广西壮族自治区钦州市浦北县2023-2024学年七年级上学期1月期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. 如图,是一个几何体的展开图,则该几何体是( )
 A、长方体 B、圆柱 C、球 D、圆锥2. 如果零上2℃记作+2℃,那么零下3℃记作()A、-3℃ B、-2℃ C、+3℃ D、+2℃3. 下列各数中,最小的数是( )A、 B、0 C、 D、4. (-4)5表示( )A、5乘以 B、5个连加 C、5个连乘 D、5个4连乘5. 下列各式中,是一元一次方程的是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 买一个足球需元,买一个篮球需元,则买5个足球和4个篮球共需( )A、元 B、元 C、元 D、元8. 如图,是的平分线, , , 则的大小为( )
A、长方体 B、圆柱 C、球 D、圆锥2. 如果零上2℃记作+2℃,那么零下3℃记作()A、-3℃ B、-2℃ C、+3℃ D、+2℃3. 下列各数中,最小的数是( )A、 B、0 C、 D、4. (-4)5表示( )A、5乘以 B、5个连加 C、5个连乘 D、5个4连乘5. 下列各式中,是一元一次方程的是( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 买一个足球需元,买一个篮球需元,则买5个足球和4个篮球共需( )A、元 B、元 C、元 D、元8. 如图,是的平分线, , , 则的大小为( )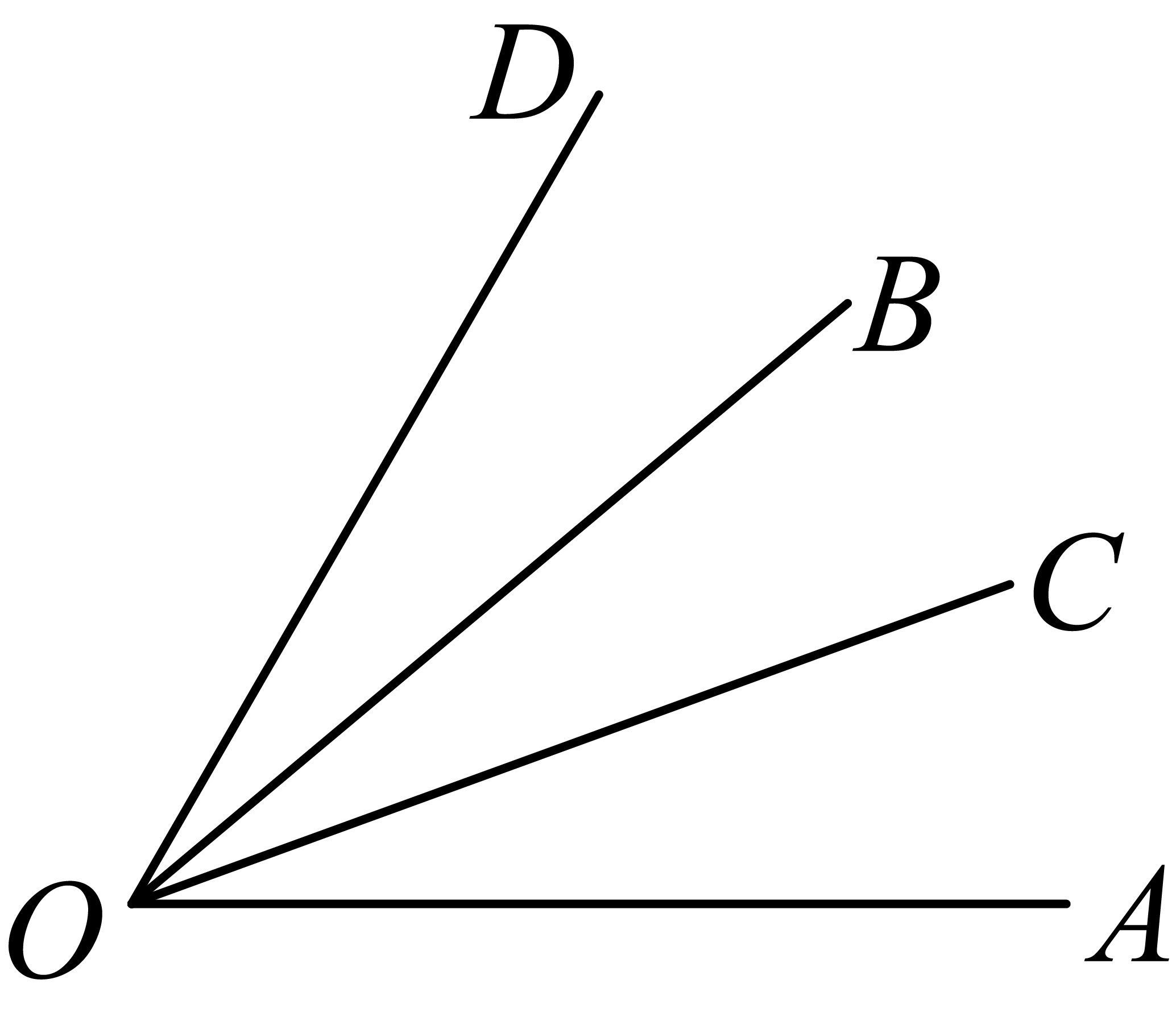 A、 B、 C、 D、9. 如图, , 是线段 上的两点,且 是线段 的中点,若 , ,则 的长为( )
A、 B、 C、 D、9. 如图, , 是线段 上的两点,且 是线段 的中点,若 , ,则 的长为( ) A、 B、 C、 D、10. 根据等式的性质,下列变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么11. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为
A、 B、 C、 D、10. 根据等式的性质,下列变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么11. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为 天,则可列方程为( ) A、 B、 C、 D、12. 有理数a、b、c在数轴上的对应点的位置如图所示,下列式子:①|b|<|c|,②b+c<0,③a﹣c>0;④ac<0,其中正确的有( )
天,则可列方程为( ) A、 B、 C、 D、12. 有理数a、b、c在数轴上的对应点的位置如图所示,下列式子:①|b|<|c|,②b+c<0,③a﹣c>0;④ac<0,其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 将数1250000用科学记数法表示为 .14. 已知∠α=38°12',则∠α的余角是 .15. 若与是同类项,则的值为 .16. 如图,已知点在点的西北方向,点在点的北偏东方向,那么的度数为 .
 17. 幻方,最早源于我国,古人称之为纵横图,幻方有完全幻方、乘幻方、高次幻方、反幻方等.在如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中的值为 .
17. 幻方,最早源于我国,古人称之为纵横图,幻方有完全幻方、乘幻方、高次幻方、反幻方等.在如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中的值为 .2
4
3
5
0
18. 如图,是用火柴棒拼成的图形,则第n个图形需根火柴棒.
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算:(1)、;(2)、 .20.(1)、解方程: .(2)、解方程:21. 先化简,再求值:2(a2+a﹣b)﹣(a﹣2b),其中a=﹣1.22. 已知有理数满足条件: , , , 求的值.23. 如图,已知直线和直线外三点A,B,C,按下列要求画图.
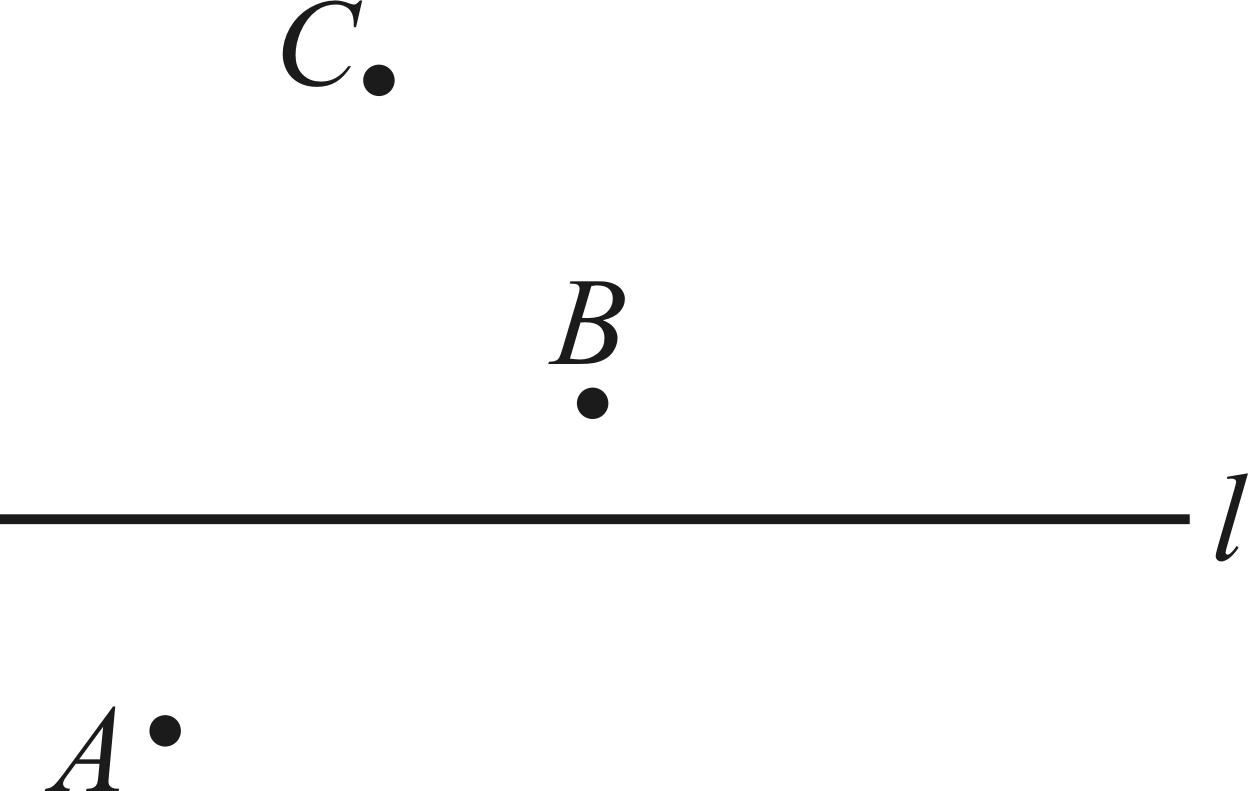 (1)、画射线 , 连接;(2)、反向延长线段 , 在延长线上作线段;(3)、在直线上确定点E,使得最小.24. 某超市销售某品牌的羽毛球拍和羽毛球,羽毛球拍每副定价102元,羽毛球每桶定价30元.店庆期间该超市开展促销活动,活动期间向顾客提供两种优惠方案.
(1)、画射线 , 连接;(2)、反向延长线段 , 在延长线上作线段;(3)、在直线上确定点E,使得最小.24. 某超市销售某品牌的羽毛球拍和羽毛球,羽毛球拍每副定价102元,羽毛球每桶定价30元.店庆期间该超市开展促销活动,活动期间向顾客提供两种优惠方案.方案一:买一副羽毛球拍送一桶羽毛球;
方案二:羽毛球拍和羽毛球都按定价的90%付款.
现某羽毛球培训学校要到该超市购买羽毛球拍5副,羽毛球x桶(x>5):
(1)、 若该校按方案一购买,需付款元:(用含x的代数式表示),若该校按方案二购买,需付款元.(用含x的代数式表示);
(2)、当x取何值时,两种方案一样优惠?(3)、当x=30时,通过计算说明按以上两种万案时哪种方案购买较为合算?你能给出一种更为省钱的购买方法吗?请写出你的购买方法,并计算需付款多少元?25. 观察下列每对数在数轴上的对应点间的距离:3与5,4与 , 与 . 并回答下列各题: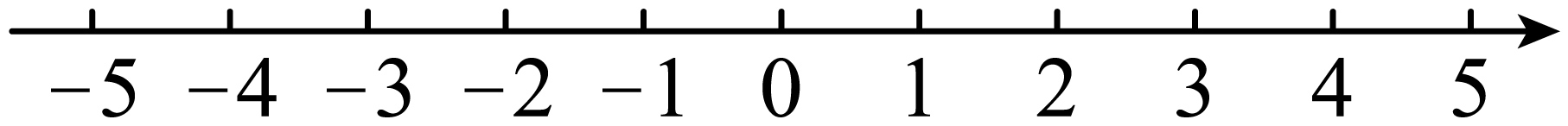 (1)、数轴上表示4和两点间的距离是;表示和两点间的距离是 .(2)、若数轴上的点A表示的数为x,点B表示的数为 .
(1)、数轴上表示4和两点间的距离是;表示和两点间的距离是 .(2)、若数轴上的点A表示的数为x,点B表示的数为 .①数轴上A、B两点间的距离可以表示为 (用含x的代数式表示);
②如果数轴上A、B两点间的距离为 , 求x的值.
(3)、直接写出代数式的最小值为 .26. 综合与实践问题情境
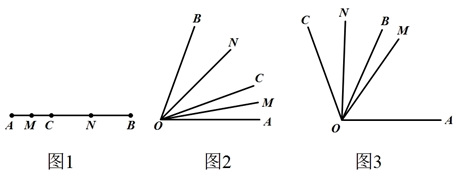
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动,发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点C是线段AB上的一点,M是AC的中点,N是BC的中点.
 (1)、问题探究
(1)、问题探究①若AB=6,AC=2,求MN的长度.(写出计算过程)
②若AB=a , AC=b , 则MN= ▲ . (直接写出结果)
(2)、继续探究“创新”小组的同学类比想到:如图2,已知∠AOB=70°,在角的内部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON .
③若∠AOC=20°,求∠MON的度数.(写出计算过程)
④若∠AOC=m , 则∠MON= ▲ . (直接写出结果)
(3)、深入探究“慎密”小组在“创新”小组的基础上提出:如图3,若∠AOB=n , 在角的外部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON , 若∠AOC=m , 则∠MON= . (直接写出结果)