广西壮族自治区钦州市浦北县2023-2024学年九年级上学期1月期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. 下列关系式中,是的反比例函数的是( )A、 B、 C、 D、2. 与点关于原点对称的点的坐标是( )A、 B、 C、 D、3. 下列事件中,是必然事件的是( )A、明天太阳从东方升起 B、五边形的外角和等于 C、购买一张彩票,中奖 D、随意翻开数学课本的某页,这页的页码是偶数4. 如图,在 中, , ,则 的度数是( )
 A、10° B、20° C、30° D、40°5. 若方程没有实数根,则k值可以是( )A、 B、 C、 D、6. 如图,转盘中四个扇形的面积都相等,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( )
A、10° B、20° C、30° D、40°5. 若方程没有实数根,则k值可以是( )A、 B、 C、 D、6. 如图,转盘中四个扇形的面积都相等,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( )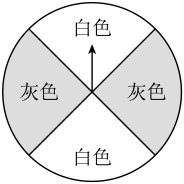 A、 B、 C、 D、7. 如图,的半径为13,弦 , 于点 , 则的长为( )
A、 B、 C、 D、7. 如图,的半径为13,弦 , 于点 , 则的长为( ) A、10 B、6 C、5 D、128. 将抛物线 通过一次平移可得到抛物线 .对这一平移过程描述正确的是( )A、向右平移3个单位长度 B、向上平移3个单位长度 C、向左平移3个单位长度 D、向下平移3个单位长度9. 如图,在等边△ABC中,AB=6,点D是BC的中点,将△ABD绕点A逆时针旋转后得到△ACE,那么线段DE的长为( )
A、10 B、6 C、5 D、128. 将抛物线 通过一次平移可得到抛物线 .对这一平移过程描述正确的是( )A、向右平移3个单位长度 B、向上平移3个单位长度 C、向左平移3个单位长度 D、向下平移3个单位长度9. 如图,在等边△ABC中,AB=6,点D是BC的中点,将△ABD绕点A逆时针旋转后得到△ACE,那么线段DE的长为( ) A、 B、6 C、 D、10. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了 , 另一边减少了 , 剩余一块面积为的矩形空地.设原正方形空地的边长为 , 则下面所列方程正确的是( )
A、 B、6 C、 D、10. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了 , 另一边减少了 , 剩余一块面积为的矩形空地.设原正方形空地的边长为 , 则下面所列方程正确的是( ) A、 B、 C、 D、11. 某品牌自动饮水机,开机加热时每分钟上升 , 加热到 , 停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中正确的是( )
A、 B、 C、 D、11. 某品牌自动饮水机,开机加热时每分钟上升 , 加热到 , 停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中正确的是( ) A、上午点接通电源,可以保证当天能喝到不超过的水 B、水温下降过程中,与的函数关系式是 C、水温从加热到 , 需要 D、水温不低于的时间为12. 如图,在四边形中,点 , , , 分别是 , , , 的中点,若四边形是矩形,且其周长是20,则四边形的面积的最大值是( )
A、上午点接通电源,可以保证当天能喝到不超过的水 B、水温下降过程中,与的函数关系式是 C、水温从加热到 , 需要 D、水温不低于的时间为12. 如图,在四边形中,点 , , , 分别是 , , , 的中点,若四边形是矩形,且其周长是20,则四边形的面积的最大值是( ) A、25 B、30 C、40 D、50
A、25 B、30 C、40 D、50二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 随机投掷一枚质地均匀的股子,朝上的点是3的概率是 .14. 如果一元二次方程的两根为 , , 那么 .15. 如图,的顶点都在方格纸的格点上,将绕点按顺时针方向旋转得到 , 使各顶点仍在格点上,则旋转角的度数是 .
 16. 已知圆锥的高h=2cm,底面半径r=2cm,则圆锥的全面积是 .17. 下列是关于抛物线的性质:①图象开口向上;②对称轴是直线;③当时,随的增大而减小;④当或时, , 其中正确的是(填写序号).18. 如图,三个顶点分别在反比例函数 , 的图象上,若 , 轴,轴, , 则k的值为 .
16. 已知圆锥的高h=2cm,底面半径r=2cm,则圆锥的全面积是 .17. 下列是关于抛物线的性质:①图象开口向上;②对称轴是直线;③当时,随的增大而减小;④当或时, , 其中正确的是(填写序号).18. 如图,三个顶点分别在反比例函数 , 的图象上,若 , 轴,轴, , 则k的值为 .
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 解方程: .20. 如图,和关于点成中心对称.
 (1)、找出它们的对称中心;(2)、若 , 求的周长;21. 一只不透明的袋子中装有4个小球,分别标有编号 , 这些小球除编号外都相同.(1)、搅匀后从中任意摸出1个球,这个球的编号是2的概率为 .(2)、搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大1的概率是多少?(用画树状图或列表的方法说明)22. 直线与双曲线相交于点 , 与轴交于点 .
(1)、找出它们的对称中心;(2)、若 , 求的周长;21. 一只不透明的袋子中装有4个小球,分别标有编号 , 这些小球除编号外都相同.(1)、搅匀后从中任意摸出1个球,这个球的编号是2的概率为 .(2)、搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大1的概率是多少?(用画树状图或列表的方法说明)22. 直线与双曲线相交于点 , 与轴交于点 .
(1)、求双曲线表达式;(2)、请在平面直角坐标系中直接画出直线与双曲线的图象.23. 如图,隧道的截面由抛物线和长方形构成.长方形的长为16m , 宽为6m , 抛物线的最高点C离路面AA1的距离为8m .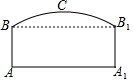 (1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?24. 如图,为的直径,点在直径上(点与 , 两点不重合), , 点在上且满足 , 连接并延长到点,使 .
(1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?24. 如图,为的直径,点在直径上(点与 , 两点不重合), , 点在上且满足 , 连接并延长到点,使 . (1)、求证:是的切线;(2)、当时,求半径的长.25. 已知抛物线 .
(1)、求证:是的切线;(2)、当时,求半径的长.25. 已知抛物线 .
(1)、抛物线的对称轴为直线;抛物线与轴的交点坐标为;(2)、若抛物线的顶点恰好在轴上,写出抛物线的顶点坐标,求它的解析式并画出函数图象;(3)、在(2)的条件下,若 , , 为抛物线上三点,且总有 , 结合图象,求的取值范围.26. 综合与探究. (1)、【问题情境】
(1)、【问题情境】数学活动课上,老师带领同学们一起探索旋转的奥秘.老师出示了一个问题:如图1所示,在中, , , 点是边上一点(),连接AD,将△ABD绕着点A按逆时针方向旋转,使AB与AC重合,得到△ACE.
连接 , 试判断的形状,并说明理由;
(2)、【深入探究】希望小组受此启发,如图2,在线段上取一点 , 连接 , 使得 , 连接 , 发现和有一定的关系,猜想两者的数量关系,并说明理由;
(3)、智慧小组在图2的基础上继续探究,发现 , , 三条线段之间也有一定的数量关系,请写出它们的数量关系,并说明理由.