广西2024年中考数学一模考前训练卷
试卷更新日期:2024-02-21 类型:中考模拟
一、单项选择题(本大题共12小题,每小题3分,共36分)
-
1. 中国是世界上最早认识和应用负数的国家,比西方早一千多年,
在我国古代著名的数学专著《九章算术》中,首次引入负数,
如果收入100元记作元,则元表示( )
A、支出70元 B、收入70元 C、支出80元 D、收入80元2. 下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如果分式有意义,那么x的取值范围是( )A、 B、 C、 D、且4. 不等式组 的解集在数轴上表示为 ( )A、
3. 如果分式有意义,那么x的取值范围是( )A、 B、 C、 D、且4. 不等式组 的解集在数轴上表示为 ( )A、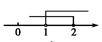 B、
B、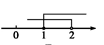 C、
C、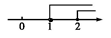 D、
D、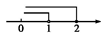 5. 如图, , , 则的度数为( )
5. 如图, , , 则的度数为( )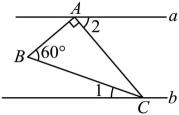 A、 B、 C、 D、6. 下列计算正确的( )A、 B、 C、 D、7. 若点在反比例函数的图象上,
A、 B、 C、 D、6. 下列计算正确的( )A、 B、 C、 D、7. 若点在反比例函数的图象上,则的大小关系是( )
A、 B、 C、 D、8. 将抛物线 向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )A、 B、 C、 D、9. 关于x的方程有实数根,则k的取值范围是( )A、 B、 C、 D、且10. 已知 , , 则的值为( )A、0 B、 C、4 D、11. 如图,ABCD是一张矩形纸片,点E是AD边上的一点,将纸片沿直线BE翻折,点A落在DC边上的点F处,若AB=10,AD=8,则DE的长为( )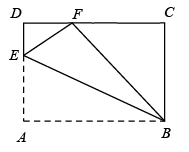 A、6 B、5 C、4 D、312. 如图,已知开口向上的抛物线与轴交于点 , 对称轴为直线 . 下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )
A、6 B、5 C、4 D、312. 如图,已知开口向上的抛物线与轴交于点 , 对称轴为直线 . 下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )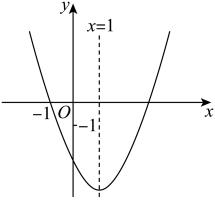 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 若式子 在实数范围内有意义,则x的取值范围是 .14. 因式分解:3x3﹣12x= .
15. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.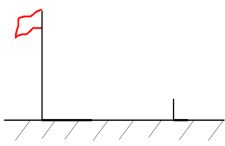 16. 代数式与代数式的值相等,则x= .17. 人字梯为现代家庭常用的工具.如图,若 , 的长都为 , 当时,人字梯顶端离地面的高度为 . (结果保留小数点后1位)(参考数据:)
16. 代数式与代数式的值相等,则x= .17. 人字梯为现代家庭常用的工具.如图,若 , 的长都为 , 当时,人字梯顶端离地面的高度为 . (结果保留小数点后1位)(参考数据:)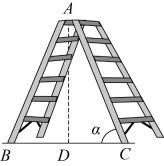 18. 如图,已知正方形的边长为4,M是对角线上的一个动点(不与B , D重合),连接 , 过M分别作的垂线段垂足分别为E , F , 则的最小值是 .
18. 如图,已知正方形的边长为4,M是对角线上的一个动点(不与B , D重合),连接 , 过M分别作的垂线段垂足分别为E , F , 则的最小值是 .
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 计算: .20. 解分式方程: .21. 如图,在中, , .
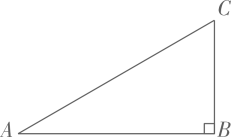 (1)、在斜边上求作线段 , 使 , 连接;
(1)、在斜边上求作线段 , 使 , 连接;(要求:尺规作图并保留作图痕迹,不写作法,标明字母)
(2)、若 , 求的长.22. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校响应号召,开展了“读红色经典,传革命精神”为主题的读书活动,学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查,并对所有随机抽取的学生的读书量(单位:本)进行了统计.根据调查结果,绘制了不完整的统计表和扇形统计图.
读书量
本
本
本
本
本
人数
人
人
人
人
 (1)、本次调查共抽取学生人,学生读书量的众数是 , 中位数是 , 扇形统计图中“本”部分所对应的圆心角的度数为;(2)、求该样本中平均每人的读书量;(3)、已知该校有名学生,请估计该校学生中,五月份读书量不少于“本”的学生人数.(4)、后来又抽取几名学生的读书量,他们的读书量都不低于本,把这几名学生的读书量与原来的数据一起统计中位数没有发生改变,则最多又抽取名学生.23. 如图中, , 平分交于 , 以为圆心,为半径作交于 .
(1)、本次调查共抽取学生人,学生读书量的众数是 , 中位数是 , 扇形统计图中“本”部分所对应的圆心角的度数为;(2)、求该样本中平均每人的读书量;(3)、已知该校有名学生,请估计该校学生中,五月份读书量不少于“本”的学生人数.(4)、后来又抽取几名学生的读书量,他们的读书量都不低于本,把这几名学生的读书量与原来的数据一起统计中位数没有发生改变,则最多又抽取名学生.23. 如图中, , 平分交于 , 以为圆心,为半径作交于 .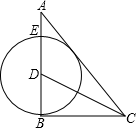 (1)、 求证:与相切;(2)、若 , , 试求的长.24. 为鼓励同学们参加主题为“阅读润泽心灵,文字见证成长”的读书月活动,学校计划购进一批科技类和文学类图书作为活动奖品.已知同类图书中每本书价格相同,购买2本科技类图书和3本文学类图书需131元,购买4本科技类图书和5本文学类图书需237元.(1)、科技类图书和文学类图书每本各多少元?(2)、经过评选有300名同学在活动中获奖,学校对每位获奖同学奖励一本科技类或文学类图书.如果学校用于购买奖品的资金不超过8000元,那么科技类图书最多能买多少本?25. 如图,已知抛物线与一直线相交于 , 两点,与y轴交于点N .
(1)、 求证:与相切;(2)、若 , , 试求的长.24. 为鼓励同学们参加主题为“阅读润泽心灵,文字见证成长”的读书月活动,学校计划购进一批科技类和文学类图书作为活动奖品.已知同类图书中每本书价格相同,购买2本科技类图书和3本文学类图书需131元,购买4本科技类图书和5本文学类图书需237元.(1)、科技类图书和文学类图书每本各多少元?(2)、经过评选有300名同学在活动中获奖,学校对每位获奖同学奖励一本科技类或文学类图书.如果学校用于购买奖品的资金不超过8000元,那么科技类图书最多能买多少本?25. 如图,已知抛物线与一直线相交于 , 两点,与y轴交于点N . (1)、求抛物线的函数关系式;(2)、求直线AC的函数关系式;(3)、若P是抛物线上位于直线AC上方的一个动点.求面积的最大值.26.(1)、【问题发现】如图1所示,和均为正三角形,B、D、E三点共线.猜想线段、之间的数量关系为;;
(1)、求抛物线的函数关系式;(2)、求直线AC的函数关系式;(3)、若P是抛物线上位于直线AC上方的一个动点.求面积的最大值.26.(1)、【问题发现】如图1所示,和均为正三角形,B、D、E三点共线.猜想线段、之间的数量关系为;;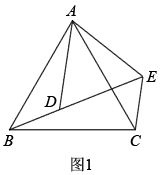 (2)、【类比探究】
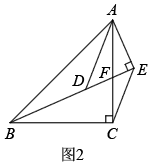
(2)、【类比探究】如图2所示,和均为等腰直角三角形, , , , B、D、E三点共线,线段、交于点F.此时,线段、之间的数量关系是什么?请写出证明过程并求出的度数;
 (3)、【拓展延伸】
(3)、【拓展延伸】如图3所示,在中, , , , 为的中位线,将绕点A顺时针方向旋转,当所在直线经过点B时,请直接写出的长.