广东省汕头市潮南区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 当 $x = - 1$ 时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x - 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x + 1}$

查看试题解析
2. 七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{3} \cdot a^{3} = a^{6}$ C、 $a^{9} \div a^{3} = a^{3}$ D、 $(a b)^{3} = a b^{3}$

查看试题解析
4. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )

A、4 B、5 C、6 D、7

查看试题解析
5. 已知点M（3，－1）关于y轴对称的的对称点N的坐标为（a＋b，1－b），则a^b的值为（）

A、10 B、25 C、－3 D、32

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A = 7 0^{∘}$ ， $∠ C = 3 0^{∘}$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点 $D$ ， $D E / / A B$ ，交 $B C$ 于点 $E$ ，则 $∠ B D E$ 的度数是（）

A、 $3 0^{∘}$ B、 $4 0^{∘}$ C、 $5 0^{∘}$ D、 $6 0^{∘}$

查看试题解析
7. 若x+m与2﹣x的乘积中不含x的一次项，则实数m的值为（）

A、﹣2 B、2 C、0 D、1

查看试题解析
8. 如图，已知在 $△ A B C$ 中， $C D$ 是 $A B$ 边上的高线， $B E$ 平分 $∠ A B C$ ，交 $C D$ 于点 $E$ ， $B C = 5$ ， $D E = 2$ ，则 $△ B C E$ 的面积等于（）．

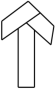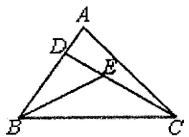A、8 B、6 C、5 D、4

查看试题解析
9. 若m－n＝2，则代数式 $\frac{m^{2} - n^{2}}{m} \cdot \frac{2 m}{m + n}$ 的值是（）

A、－2 B、2 C、－4 D、4

查看试题解析
10. 如图，等边 $△ A B C$ 中，D为AC中点，点P、Q分别为AB、AD上的点， $B P = A Q = 4$ ， $Q D = 3$ ，在BD上有一动点E，则 $P E + Q E$ 的最小值为（）

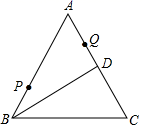A、7 B、8 C、10 D、12

查看试题解析

二、填空题（每小题3分，共15分）

11. 原子很小， $1$ 个氧原子的直径大约为 $0.000000000148 m$ ，将 $0.000000000148$ 用科学记数法表示为.

查看试题解析
12. 已知 $a = 7 - 3 b$ ，则代数式 $a^{2} + 6 a b + 9 b^{2}$ 的值为.

查看试题解析
13. 一个三角形两边长分别为3和8，第三边长为奇数，则第三边长为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $D E$ 是 $B C$ 的垂直平分线，若 $A B = 6$ ， $A C = 9$ ，则 $△ A B D$ 的周长是．

查看试题解析
15. 若分式方程 $\frac{3 x - a}{x^{2} - 2 x}$ ＋ $\frac{1}{x - 2}$ ＝ $\frac{2}{x}$ 有增根，则实数a的取值是．

查看试题解析

三、解答题（一）（每小题6分，共24分）

16. 计算： ${(- \frac{1}{2})}^{- 2} - {(- \frac{2}{3})}^{2022} \times {(\frac{3}{2})}^{2023} - 2^{2} + (3 - π)^{0}$ ．

查看试题解析
17. 计算： $a (2 a + 3 b) + {(a - b)}^{2}$ ；

查看试题解析
18. 如图、在平面直角坐标系中， $△ A B C$ 的三个顶点的坐标分别为 $A (4 ， 1)$ ， $B (2 ， 3)$ ， $C (1 ， 2)$ ，画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析
19. 解方程： $\frac{x}{x - 1} - \frac{2}{x} = 1$ ．

查看试题解析

四、解答题（二）（每小题7分，共21分）

20. 如图， $B E$ 是 $△ A B C$ 的角平分线，在 $A B$ 上取点 $D$ ，使 $D B = D E$ .

(1)、求证： $D E // B C$ .

(2)、若 $∠ A = 65 °$ ， $∠ A E D = 45 °$ ，求 $∠ E B C$ 的度数.

查看试题解析
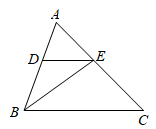21. 接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂．为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂．

(1)、求该厂当前参加生产的工人有多少人？

(2)、生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时．若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？

查看试题解析
22. 校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形ABCD，其中 AB＝CD＝2米，AD＝BC＝3米，∠B＝ $30 °$

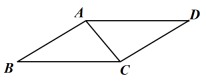(1)、求证：△ABC≌△CDA ；

(2)、求草坪造型的面积.

查看试题解析

五、解答题（三）（每小题10分，共30分）

23. 八年级课外兴趣小组活动时，老师提出了如下问题：将 $2 a - 3 a b - 4 + 6 b$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $= (2 a - 3 a b) - (4 - 6 b) = a (2 - 3 b) - 2 (2 - 3 b) = (2 - 3 b) (a - 2)$ ；
解法二：原式 $= (2 a - 4) - (3 a b - 6 b) = 2 (a - 2) - 3 b (a - 2) = (a - 2) (2 - 3 b)$ ．
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

(1)、【类比】请用分组分解法将 $x^{2} - a^{2} + x + a$ 因式分解；

(2)、【挑战】请用分组分解法将 $a x + a^{2} - 2 a b - b x + b^{2}$ 因式分解；

(3)、若 $a^{2} + b^{2} = 9$ ， $a - b = 2$ ，请用分组分解法先将 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值．

查看试题解析
24. 如图，已知：在△ABC中，AC=BC=8，∠ACB=120°，将一块足够大的直角三角尺PMN（∠M=90°，∠MPN=30°）按如图放置，顶点P在线段AB上滑动，三角尺的直角边PM始终经过点C，并且与CB的夹角∠PCB=α，斜边PN交AC于点D．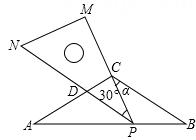

(1)、当PN∥BC时，判断△ACP的形状，并说明理由；

(2)、点P在滑动时，当AP长为多少时，△ADP与△BPC全等，并说明理由；

(3)、点P在滑动时，△PCD的形状可以是等腰三角形吗？若可以，
请直接写出夹角α的大小；若不可以，请说明理由．

查看试题解析
25. 在等边 $△ A B C$ 的顶点 $A$ ， $C$ 处各有一只蜗牛，它们同时出发，分别以相同的速度由 $A$ 向 $B$ 和由 $C$ 向 $A$ 爬行，经过 $t$ 分钟后，它们分别爬行到 $D$ ， $E$ 处，请问：

(1)、如图1，爬行过程中， $C D$ 和 $B E$ 的数量关系是；

(2)、如图2，当蜗牛们分别爬行到线段 $A B$ ， $C A$ 的延长线上的 $D$ ， $E$ 处时，若 $E B$ 的延长线与 $C D$ 交于点 $Q$ ，其他条件不变，蜗牛爬行过程中 $∠ C Q E$ 的大小将会保持不变，请你证明： $∠ C Q E = 60 °$ ；

(3)、如图3，如果将原题中“由 $C$ 向 $A$ 爬行”改为“沿着线段 $B C$ 的延长线爬行，连接 $D E$ 交 $A C$ 于 $F$ ”，其他条件不变，求证： $D F = E F$ ．

查看试题解析