广东省江门市新会区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本题共10小题,每小题3分,共30分):
-
1. 若关于x的方程(m﹣2)x2+mx﹣1=0是一元二次方程,则m的取值范围是( )A、m≠2 B、m=2 C、m≥2 D、m≠02. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. 把抛物线向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为( )A、 B、 C、 D、5. 在平面直角坐标系中,⊙O的半径为5,圆心在原点O,则P(﹣3,4)与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定6. 下列成语所描述的事件是必然发生的是( )A、水中捞月 B、拔苗助长 C、守株待兔 D、瓮中捉鳖7. 广州南站到江门站距约则动车由子广州南站行驶到江门站所用时间(小时)与行驶速度(千米/时)之间的函数图象大致是( )A、
3. 一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. 把抛物线向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为( )A、 B、 C、 D、5. 在平面直角坐标系中,⊙O的半径为5,圆心在原点O,则P(﹣3,4)与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定6. 下列成语所描述的事件是必然发生的是( )A、水中捞月 B、拔苗助长 C、守株待兔 D、瓮中捉鳖7. 广州南站到江门站距约则动车由子广州南站行驶到江门站所用时间(小时)与行驶速度(千米/时)之间的函数图象大致是( )A、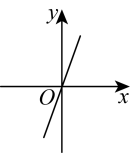 B、
B、 C、
C、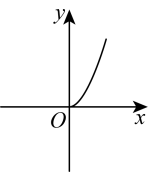 D、
D、 8. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( )
8. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( ) A、或 B、或 C、或 D、或9. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A、或 B、或 C、或 D、或9. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( ) A、 B、 C、3 D、210. 如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(- ,y1),( ,y2)是抛物线上两点,则y1<y2 , 其中结论正确的是( )
A、 B、 C、3 D、210. 如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(- ,y1),( ,y2)是抛物线上两点,则y1<y2 , 其中结论正确的是( ) A、①② B、②③ C、②④ D、①③④
A、①② B、②③ C、②④ D、①③④二、填空题(本题共6小题,每小题3分,共18分):
-
11. 写出以为其中一根的一个一元二次方程 . (写出一个即可)12. 若反比例函数的图像径过点 , 则的值为 .13. 二维码具有储存量大,保密性高,追踪性高,成本便宜等特性,如图是一张边长为5 cm的正方形二维码的示意图,在正方形区域内随机掷点,通过大量重复试验,发现点落在黑色部分的频率稳定在0.7左右,由此可以估计该二维码黑色部分的总面积为 .
 14. 已知圆锥的底面半径为 , 将其侧面展开后得到的扇形圆心角为 , 则此圆锥的母线长为 .15. 《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是步.16. 对于两个不相等的实数 , , 我们规定符号表示 , 中较大的数,如: .(1)、方程的解为;(2)、方程的解为 .
14. 已知圆锥的底面半径为 , 将其侧面展开后得到的扇形圆心角为 , 则此圆锥的母线长为 .15. 《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是步.16. 对于两个不相等的实数 , , 我们规定符号表示 , 中较大的数,如: .(1)、方程的解为;(2)、方程的解为 .三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
-
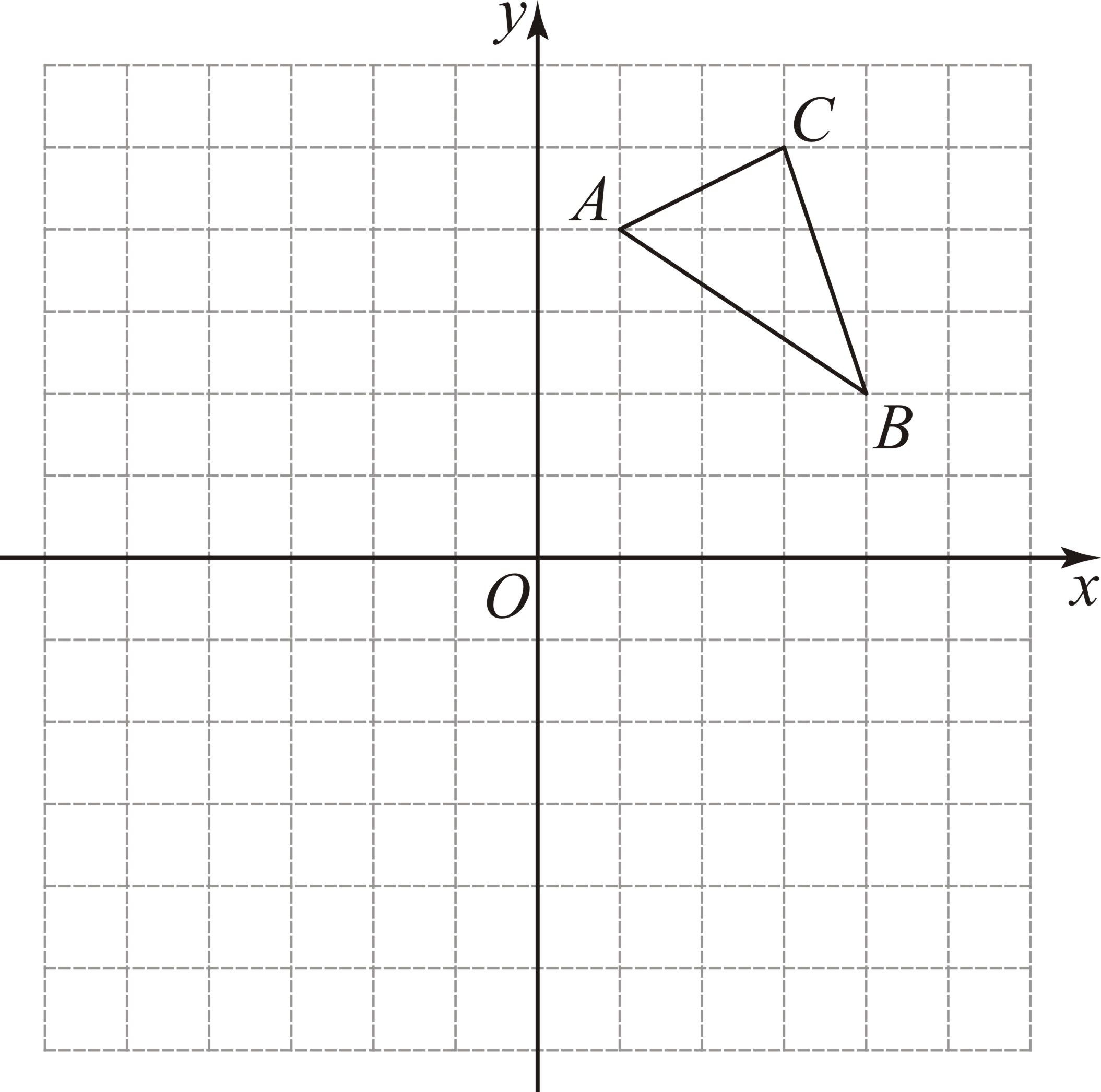
17. 解方程:3x(x-2)=4(2-x)18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , (每个方格的边长均为1个单位长度).将绕点逆时针旋转90°,画出旋转后得到的 .
 19. 如图, , 是的切线, , 为切点,是的直径, , 求和的度数.
19. 如图, , 是的切线, , 为切点,是的直径, , 求和的度数.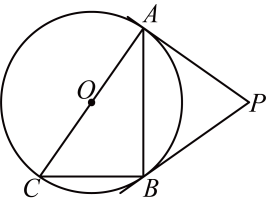 20. 如图,把一个直角三角形绕着30°角的顶点顺时针旋转,使得点与的延长线上的点重合.
20. 如图,把一个直角三角形绕着30°角的顶点顺时针旋转,使得点与的延长线上的点重合.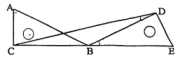 (1)、三角形旋转了多少度?(2)、连接 , 求的度数.21. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)、三角形旋转了多少度?(2)、连接 , 求的度数.21. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)22. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.23. 如图,已知 , 是一次函数的图象和反比例函数的图象的两个交点.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)22. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.23. 如图,已知 , 是一次函数的图象和反比例函数的图象的两个交点.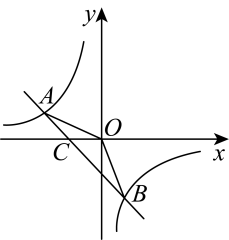 (1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、求不等式的解集(请直接写出答案).24. 用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.(1)、求y关于x的函数关系式;(2)、当x为何值时,围成的养鸡场面积为60平方米?(3)、能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.25. 如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)、求反比例函数和一次函数的解析式;(2)、求的面积;(3)、求不等式的解集(请直接写出答案).24. 用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.(1)、求y关于x的函数关系式;(2)、当x为何值时,围成的养鸡场面积为60平方米?(3)、能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.25. 如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).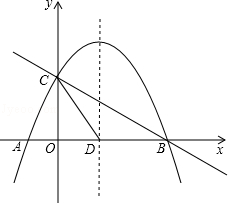 (1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
(1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.