广东省深圳市福田区2023-2024学年八年级上学期数学期末模考试卷
试卷更新日期:2024-02-21 类型:期末考试
一、选择题
-
1. 9的平方根是( )A、3 B、±3 C、﹣3 D、±2. 在平面直角坐标系中,点到原点的距离是( )A、5 B、3 C、4 D、73. 某企业车间有名工人,某一天他们生产的机器零件个数统计如表:
零件个数(个)
6
7
8
人数(人)
9
8
3
表中表示零件个数的数据中,众数、中位数分别是( )
A、7个,7个 B、6个,7个 C、个,个 D、8个,6个4. 已知 , 是关于x的函数图象上的两点,当时, , 则m的取值范围是( )A、 B、 C、 D、5. 已知方程组 的解满足 ,则 的值为( )A、7 B、 C、1 D、6. 如图,在△ABC中,AB=AC , MN是AB的垂直平分线,△BNC的周长是24cm,BC=10cm,则AB的长是( )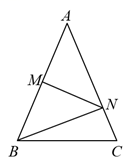 A、17cm B、12cm C、14cm D、34cm7. 《九章算术》中记载一题目,译文如下,今有人合伙购物,每人出8钱,会多3钱;
A、17cm B、12cm C、14cm D、34cm7. 《九章算术》中记载一题目,译文如下,今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱,问人数、物价各是多少?设合伙人数为人,物价为钱,
以下列出的方程组正确的是( )
A、 B、 C、 D、8. 函数与( , )在同一坐标系中的图象可能是( )A、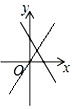 B、
B、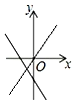 C、
C、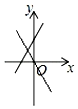 D、
D、 9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( ) A、 B、3 C、4 D、510. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
A、 B、3 C、4 D、510. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A , B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后1.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或 .
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题(本部分共5小题,每小题3分,共15分,请将正确的答案填在答题卡上).
-
11. 点与点B关于y轴对称,则点B的坐标是 .12. 人数相同的甲乙两班学生在同一次数学单元测试中,班级平均分和方差如下:=85,s甲2=25,s乙2=16,则成绩较为稳定的班级是 .13. 如图,已知函数 和 的图象交于点P,则二元一次方程组 的解是 .
 14. 有一个数值转换器,流程如下:
14. 有一个数值转换器,流程如下:
当输入的x值为时,输出的y值是 .
15. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,若CD=1,则BD的长是 .
三、解答题(本大题共7题.其中16题6分,17题7分,18题7分,19题8分,20题8分,21题10分,22题9分,共55分).
-
16.(1)、化简(2)、解方程组 .17. 如图,D、C、F、B四点在一条直线上,AB=DE , AC⊥BD , EF⊥BD , 垂足分别为点C、点F , CD=BF.求证:AB∥DE.
 18. 某校开展了以“追梦新时代”为主题的读书活动,并对本校八年级学生12月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,
18. 某校开展了以“追梦新时代”为主题的读书活动,并对本校八年级学生12月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如图所示.

根据以上信息,解答下列问题;
(1)、求出随机被抽查的学生总数,并补全不完整的条形统计图;(2)、填写本次所抽取学生12月份“读书量”的中位数为 本,众数为 本;(3)、求本次所抽取学生12月份“读书量”的平均数.19. 甲、乙两人参加从地到地的长跑比赛,两人在比赛时所跑的路程(米)与时间(分钟)之间的函数关系如图所示,请你根据图象,回答下列问题: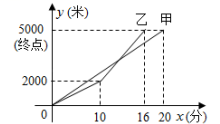 (1)、先到达终点(填“甲”或“乙”);(2)、根据图象,求出甲的函数表达式;(3)、求何时甲乙相遇?(4)、根据图象,直接写出何时甲与乙相距250米.20. 五和超市购进 、 两种饮料共200箱,两种饮料的成本与销售价如下表:
(1)、先到达终点(填“甲”或“乙”);(2)、根据图象,求出甲的函数表达式;(3)、求何时甲乙相遇?(4)、根据图象,直接写出何时甲与乙相距250米.20. 五和超市购进 、 两种饮料共200箱,两种饮料的成本与销售价如下表:饮料
成本(元/箱)
销售价(元/箱)
25
35
35
50
(1)、若该超市花了6500元进货,求购进 、 两种饮料各多少箱?(2)、设购进 种饮料 箱( ),200箱饮料全部卖完可获利润 元,求 与 的函数关系式,并求购进 种饮料多少箱时,可获得最大利润,最大利润是多少?

