广东省汕头市澄海区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 的倒数是( )A、 B、 C、 D、2. 人教版初中数学教科书共六册,总字数是978000,用科学记数法可将978000表示为( )A、 B、 C、 D、3. 如图所示几何体的左视图是( )
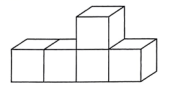 A、
A、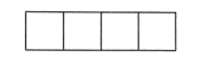 B、
B、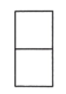 C、
C、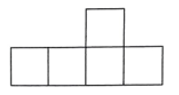 D、
D、 4. 下列等式变形错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 下面合并同类项正确的是( )A、 B、 C、 D、6. 如图,与相交于点 , , 垂足为 , 若 , 则( )
4. 下列等式变形错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 下面合并同类项正确的是( )A、 B、 C、 D、6. 如图,与相交于点 , , 垂足为 , 若 , 则( )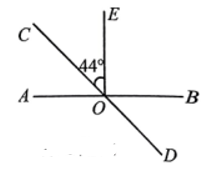 A、44° B、46° C、134° D、136°7. 一个两位数,个位上的数是1,十位上的数是 , 把1与对调得到一个新两位数,若新两位数比原两位数小9,则原两位数为( )A、21 B、12 C、31 D、128. 甲乙两人在300米的环形跑道上跑步,甲每分钟跑100米,乙每分钟跑80米,若他们从同一地点同时同向出发,则( )分钟后他们第一次相遇.A、10 B、15 C、20 D、309. 已知数在数轴上的位置如下图所示,且满足 , 则下列各式:①;②;③;④ . 正确的个数有( )个
A、44° B、46° C、134° D、136°7. 一个两位数,个位上的数是1,十位上的数是 , 把1与对调得到一个新两位数,若新两位数比原两位数小9,则原两位数为( )A、21 B、12 C、31 D、128. 甲乙两人在300米的环形跑道上跑步,甲每分钟跑100米,乙每分钟跑80米,若他们从同一地点同时同向出发,则( )分钟后他们第一次相遇.A、10 B、15 C、20 D、309. 已知数在数轴上的位置如下图所示,且满足 , 则下列各式:①;②;③;④ . 正确的个数有( )个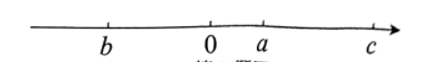 A、4 B、3 C、2 D、110. 有一组数:1、1、2、3、5、8、13、……,其中从第3个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如图)再分别依次从左到右取2个、3个、4个、5个正方形拼成如下长方形并记为①、②、③、④,相应长方形的周所如表所示:
A、4 B、3 C、2 D、110. 有一组数:1、1、2、3、5、8、13、……,其中从第3个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如图)再分别依次从左到右取2个、3个、4个、5个正方形拼成如下长方形并记为①、②、③、④,相应长方形的周所如表所示: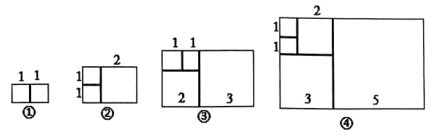
序号
①
②
③
④
周长
6
10
16
26
若按此规律继续作长方形,则序号为⑩的长方形周长是( )
A、388 B、402 C、466 D、499二、空题题(本大题共6小题,每小题3分,18分)
-
11. 若 , 则的补角是 .12. 已知是方程的解,则 .13. 若与为倒数,则的值为 .14. 已知 , 则的值为 .15. 已知 , , 平分 , 则的度数为 .16. 观察下列等式,探究其中的规律:
…………
请你归纳出: .
三、解答题(一)(本大题共3小题,每小题6分,18分)
-
17. 计算: .18. 先化简,再求值: , 其中满足 .19. 解方程: .
四、解答题(二)(本大题共3小题,每小8分,共24分)
-
20. 如图,点是线段上的三个点,是线段的中点.
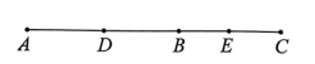 (1)、若点是的中点,且 , 求线段的长;(2)、若 , , 求线段的长.21. 用“”定义一种新运算:对于任意有理数和 , 规定 .
(1)、若点是的中点,且 , 求线段的长;(2)、若 , , 求线段的长.21. 用“”定义一种新运算:对于任意有理数和 , 规定 .如: .
(1)、求的值(2)、若 , 求的值;22. 某服装店购进甲、乙两种品牌的服装共100件,购进100件这两种品牌服装的进货款恰好为13200元,已知这两种品牌服装的进价、售价如下表所示:(利润=售价-进价)品牌
进价/(元/件)
售价/(元/件)
甲
120
150
乙
150
200
(1)、该服装店购进两品牌的服装各多少件?(2)、在实际销售过程中,服装店按原售价将购进的全部甲品牌服装和部分乙品牌服装售出后,决定将剩下的乙品牌服装打八折销售,两种品牌服装全部售完后,共获得利润2600元,求乙品牌服装按原售价售出了多少件?五、解答题(三)(本题共3小,小题10分,共30分)
-
23. 如图①,已知点为直线上一点, , 平分 .
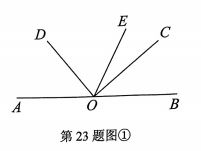
 (1)、若 , 则的度数为 .(2)、请判断与的数量关系,并说明理由;(3)、在(2)的基础上,如图,在的内部作射线 , 使平分 , 若 , 求的度数24. 一般情况下不成立,但有些数可以使得它成立,例如:等,我们称使得成立的一对数a,b为“相伴数对”,记为(a,b)(1)、若是“相伴数对”,求b的值;(2)、写两个“相伴数对” , 其中 , 且;(3)、若是“相伴数对”,求代数式的值.25. 如图,O为数轴的原点,在数轴上A点表示的数为a,B点表示的数为b,C点表示的数为c,b是最大的负整数,且|a+3|=0,c2=64.点P从点B出发以每秒2个单位长度的速度向左运动,到达点A后立刻返回运动到点C并停止.
(1)、若 , 则的度数为 .(2)、请判断与的数量关系,并说明理由;(3)、在(2)的基础上,如图,在的内部作射线 , 使平分 , 若 , 求的度数24. 一般情况下不成立,但有些数可以使得它成立,例如:等,我们称使得成立的一对数a,b为“相伴数对”,记为(a,b)(1)、若是“相伴数对”,求b的值;(2)、写两个“相伴数对” , 其中 , 且;(3)、若是“相伴数对”,求代数式的值.25. 如图,O为数轴的原点,在数轴上A点表示的数为a,B点表示的数为b,C点表示的数为c,b是最大的负整数,且|a+3|=0,c2=64.点P从点B出发以每秒2个单位长度的速度向左运动,到达点A后立刻返回运动到点C并停止. (1)、 , , ;(2)、点P从点B离开后,在点P到达点C的过程中,经过x秒钟,PA+PB+PC=12,求x的值.(3)、点P从点B出发的同时,数轴上的动点M,N分别从点A和点C同时出发,相向而行,速度分别为每秒3个单位长度和每秒4个单位长度,假设运动t秒钟时,P、M、N三点中恰好有一个点是另外两个点的中点,请求出所有满足条件的t的值.
(1)、 , , ;(2)、点P从点B离开后,在点P到达点C的过程中,经过x秒钟,PA+PB+PC=12,求x的值.(3)、点P从点B出发的同时,数轴上的动点M,N分别从点A和点C同时出发,相向而行,速度分别为每秒3个单位长度和每秒4个单位长度,假设运动t秒钟时,P、M、N三点中恰好有一个点是另外两个点的中点,请求出所有满足条件的t的值.