浙江省金华市东阳市横店八校联考2023-2024学年八年级上学期数学1月期末试卷
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本题共30分,每小题3分)
-
1. 下列“表情图”中,属于轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 函数中自变量x的取值范围是( )A、 B、 C、 D、3. 点在( )A、第四象限 B、第二象限 C、y轴上 D、x轴上4. 下面图形是用木条钉成的支架,其中不容易变形的是( )A、
2. 函数中自变量x的取值范围是( )A、 B、 C、 D、3. 点在( )A、第四象限 B、第二象限 C、y轴上 D、x轴上4. 下面图形是用木条钉成的支架,其中不容易变形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、6. 如图是某纸伞截面示意图,伞柄AP平分两条伞骨所成的角 , .若支杆DF需要更换,则所换长度应与哪一段长度相等( )
5. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、6. 如图是某纸伞截面示意图,伞柄AP平分两条伞骨所成的角 , .若支杆DF需要更换,则所换长度应与哪一段长度相等( ) A、BE B、AE C、DE D、DP7. 在以下图形中,根据尺规作图痕迹,能判断射线AD平分∠BAC的是( )
A、BE B、AE C、DE D、DP7. 在以下图形中,根据尺规作图痕迹,能判断射线AD平分∠BAC的是( )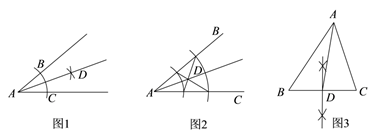 A、图1和图2 B、图1和图3 C、图3 D、图2和图38. 已知 , , 是直线(b为常数)上的三个点,则 , , 的大小关系是( )A、 B、 C、 D、9. 小明和爸爸从家里出发,沿同一路线到学校.小明匀速跑步先出发,2分钟后,爸爸骑自行车出发,匀速骑行一段时间后,在途中商店购买水果花费了5分钟,这时发现小明已经跑到前面,爸爸骑车速度增加60米/分钟,结果与小明同时到达学校.小明和爸爸两人离开家的路程s(米)与爸爸出发时间t(分钟)之间的函数图象如图所示.则下列说法错误的是( )
A、图1和图2 B、图1和图3 C、图3 D、图2和图38. 已知 , , 是直线(b为常数)上的三个点,则 , , 的大小关系是( )A、 B、 C、 D、9. 小明和爸爸从家里出发,沿同一路线到学校.小明匀速跑步先出发,2分钟后,爸爸骑自行车出发,匀速骑行一段时间后,在途中商店购买水果花费了5分钟,这时发现小明已经跑到前面,爸爸骑车速度增加60米/分钟,结果与小明同时到达学校.小明和爸爸两人离开家的路程s(米)与爸爸出发时间t(分钟)之间的函数图象如图所示.则下列说法错误的是( )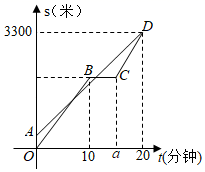 A、a=15 B、小明的速度是150米/分钟 C、爸爸从家到商店的速度为200米/分钟 D、爸爸出发7分钟追上小明10. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )
A、a=15 B、小明的速度是150米/分钟 C、爸爸从家到商店的速度为200米/分钟 D、爸爸出发7分钟追上小明10. 如图,在中, , 以的各边为边作三个正方形,点G落在上,若 , 空白部分面积为10.5,则的长为( )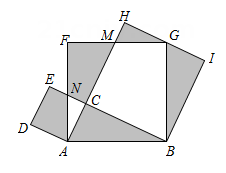 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共24分,每小题4分)
-
11. 若 , 则0(填“”或“”或“”).12. 将点向右平移3个长度单位,再向上平移2个长度单位得到点Q , 则点Q的坐标是 .13. 在一次函数的图象中,y随x的增大而增大.则k值可以是 . (写出一个答案即可)14. 一张小凳子的结构如图所示, , , 则 .
 15. 如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,则AC的长是.
15. 如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,EF=2,则AC的长是.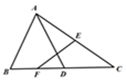 16. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .
16. 在平面直角坐标系中,已知点 , , , 在直线上找一点P , 使得 , 请写出所有满足条件的点P的坐标 .三、解答题(本题共66分)
-
17. 解不等式:(1)、;(2)、18. 如图,AF=DC , ∠BCA=∠EFD , BC=EF , 求证:△ABC≌△DEF .
 19. 如图(1),长方形纸片 , 把它沿对角线向上折叠.
19. 如图(1),长方形纸片 , 把它沿对角线向上折叠.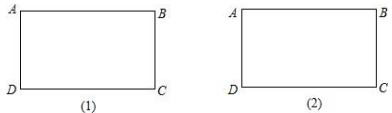 (1)、在图(2)中用实线画出折叠后得到的图形;(要求尺规作图,保留作图痕迹,不写作法)(2)、折叠后重合部分是什么图形?说明理由.20. 已知一次函数的图象经过点 , 两点.(1)、求一次函数的表达式;(2)、求这个一次函数与坐标轴围成的三角形面积;(3)、请直接写出当时的x的取值范围。21. 小聪和小慧沿图1中的风景区游览,约好在飞瀑见面.小聪驾驶电动汽车从宾馆出发,小慧也于同一时间骑电动自行车从塔林出发:图2中的图象分别表示两人离宾馆的路程与时间的函数关系,试结合图中信息回答:
(1)、在图(2)中用实线画出折叠后得到的图形;(要求尺规作图,保留作图痕迹,不写作法)(2)、折叠后重合部分是什么图形?说明理由.20. 已知一次函数的图象经过点 , 两点.(1)、求一次函数的表达式;(2)、求这个一次函数与坐标轴围成的三角形面积;(3)、请直接写出当时的x的取值范围。21. 小聪和小慧沿图1中的风景区游览,约好在飞瀑见面.小聪驾驶电动汽车从宾馆出发,小慧也于同一时间骑电动自行车从塔林出发:图2中的图象分别表示两人离宾馆的路程与时间的函数关系,试结合图中信息回答: (1)、飞瀑与宾馆相距 , 小聪出发0.2h时与宾馆的距离;(2)、若小聪出发0.2h后速度变为小慧的2倍,则小聪追上小慧时,他们是否已经过了草甸?22. 某土特产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题:
(1)、飞瀑与宾馆相距 , 小聪出发0.2h时与宾馆的距离;(2)、若小聪出发0.2h后速度变为小慧的2倍,则小聪追上小慧时,他们是否已经过了草甸?22. 某土特产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题:土特产品种
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)、设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.(2)、如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种并写出每种安排方案.(3)、若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.23. 我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点. (1)、特例感知
(1)、特例感知①等腰直角三角形 ▲ 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知为勾股高三角形,其中C为勾股顶点,是边上的高.若 , 试求线段的长度.
(2)、深入探究如图2,已知为勾股高三角形,其中C为勾股顶点且 , 是边上的高,试探究线段与的数量关系,并给予证明;
(3)、推广应用如图3,等腰为勾股高三角形,其中 , 为边上的高,过点D向边引平行线与边交于点E . 若 , 试求线段的长度.
24. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .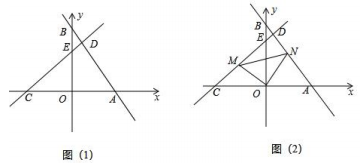 (1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .
(1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .①点M移动过程中,线段与数量关系是否不变,直接写出结论;
②当面积最小时,求点M的坐标和面积.