浙江省金华市东阳市横店八校联考试卷2023-2024学年七年级上学期数学期末试卷

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 下列比﹣2小的数是（）

A、0 B、3 C、﹣1 D、﹣3

查看试题解析
2. 在 $\frac{π}{2}$ ， $\frac{22}{7}$ ， $\sqrt{3}$ ， $\sqrt[3]{64}$ ， 0.3131131113…，3.14中，无理数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 若代数式x﹣1和3x＋7互为相反数，则x＝（）

A、3 B、﹣3 C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
4. 一条弯曲的公路改为直道，可以缩短路程，其数学道理是（）

A、线段可以比较大小 B、两点确定一条直线 C、线段有两个端点 D、两点之间，线段最短

查看试题解析
5. 2022年11月1日零时为标准时点，东阳市统计局统计，2022年末，全市常住人口108.9万人，108.9万用科学记数法表示（）

A、 $1.089 \times 1 0^{6}$ B、 $1.089 \times 1 0^{5}$ C、 $1.089 \times 1 0^{7}$ D、1089000

查看试题解析
6. 若∠1和∠2互余，∠1与∠3互补，∠3＝110°，则∠1与∠2的度数分别为（）

A、50°、40° B、70°、20° C、50°、130° D、70°、110°

查看试题解析
7. 下列说法中，正确的是（）

A、 $\frac{a + b}{3}$ 是多项式 B、 $3^{2} a b^{3}$ 的次数是6次 C、 $a^{2} + a - 1$ 的常数项是1 D、 $- \frac{2 x y}{3}$ 的系数是﹣2

查看试题解析
8. 有理数a、b在数轴上的位置如图所示，则下列说法正确的是（）

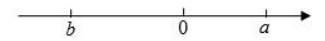A、a＋b>0 B、ab>0 C、|b|﹣|a|>0 D、b﹣a>0

查看试题解析
9. 已知：A、B、C是同一直线上的三点，点D为AB的中点，若AB＝12，BC＝7，则CD的长为（）

A、1 B、13 C、13或1 D、9.5

查看试题解析
10. 一般地，点A、B在数轴上分别表示有理数a、b ，那么A、B之间的距离可表示为|a﹣b|．下列选项中错误的是（）

A、|a|表示数a在数轴上的对应点与原点的距离 B、若满足|x﹣2|＋|x＋3|＝6|时，则x的值是﹣3.5或2.5 C、|5＋3|表示5、3在数轴上对应的两点之间的距离 D、A、B分别为数轴上两点，A点对应的数为﹣2，B点对应的数为4，则A、B两点之间的距离为6

查看试题解析

二、填空题(本题共24分，每小题4分)

11. ﹣2023的相反数是．

查看试题解析
12. 用连续的自然数填空： $< \sqrt{15} <$ ．

查看试题解析
13. $23 ° 1 4^{'} 2 4^{″}$ 化为用度表示是．

查看试题解析
14. 已知关于x的一元一次方程 $\frac{1}{2023} x + 3 = 2 x + b$ 的解为x＝﹣3，那么关于y的一元一次方程 $\frac{1}{2023} (y + 1) + 3 = 2 (y + 1) + b$ 的解为．

查看试题解析
15. 如图，AC⊥BC ， AC＝9，BC＝12，AB＝15．点A到直线BC的距离． C到直线AB的距离是．

查看试题解析
16. 如图是一个二阶幻圆模型，现将﹣1，2，﹣3，4，﹣5，6，﹣7，8分别填入圆圈内，使横、纵向以及内外圆圈上的4个数字之和都相等，则a＋b的值是．

查看试题解析

三、解答题(本题共66分)

17. 计算：

(1)、 $- 1^{2023} \times {(- 2)}^{3} - | \sqrt[3]{8} - \sqrt{9} | \div (- \frac{1}{5})$

(2)、6.18×3.2﹣0.37×61.8﹣0.618×(﹣55)

查看试题解析
18. 先化简，再求值．

(1)、 $(3 a^{2} - 7 a) + 2 (a^{2} - 3 a + 2)$ ，其中a＝1．

(2)、 $3 x y^{2} + (3 x^{2} y - 2 x y^{2}) - 4 (x y^{2} - x^{2} y)$ ，其中x＝﹣4，y＝1．

查看试题解析
19. 已知点A ， B ， C如图所示，根据要求完成下列各题．

(1)、画直线BC ，线段AB和射线CA ．

(2)、过点A画BC的垂线段AD ，垂足为D ，并量出点A到直线BC的距离为cm．(以答题纸为测量依据，结果精确到0.1cm)．

查看试题解析
20.

(1)、解方程 $x - \frac{1 - x}{3} = \frac{x + 2}{6} - 1$

(2)、在做作业时，有一个方程“ $2 y - \frac{1}{2} = \frac{1}{2} y + ■$ ”中的■没印清，小聪问老师，老师只是说：“■是一个有理数，该方程的解与方程5(x﹣1)﹣2(x﹣2)﹣4＝1的解相同，”小聪很快补上了这个常数，同学们，你们能补上这个常数吗?

查看试题解析
21. 列方程解应用题
欧尚超市恰好用3200元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的与 $\frac{1}{2}$ 少10件，甲、乙两种商品的进价和售价如表；(注：每件商品获利＝售价﹣进价)．

甲
乙
进价(元/件)
20
30
售价(元/件)
25
40

(1)、该商场购进甲、乙两种商品各多少件?

(2)、该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?

查看试题解析
22. 问题探索：如图，将一根木棒放在数轴(单位长度为1cm)上，木棒左端与数轴上的点A重合，右端与数轴上的点B重合．

(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为6，由此可得这根木棒的长为cm．

(2)、图中点A所表示的数是，点B所表示的数是．

(3)、实际应用：由(1)(2)的启发，请借助“数轴”这个工具解决下列问题：
一天，豆豆去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要35年才出生；你若是我现在这么大，我就109岁啦！”请问豆豆现在多少岁了?(画出数轴会更方便)

查看试题解析
23. 如图1，点O为直线AB上一点，过点O作射线OC ，使∠AOC＝60°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

(1)、将图1中的三角板绕点O处逆时针旋转至图2，使一边OM在∠BOC的内部．且恰好平分∠BOC ，求∠CON的度数；

(2)、在图3中，延长线段NO得到射线OD ，判断OD是否平分∠AOC ，请说明理由．

(3)、将图1中的三角板绕点O按每秒5°的速度沿顺时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC ，则t的值为． (直接写出答案)

查看试题解析
24. 已知数轴上点A与点B的距离为16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．

(1)、点A表示的数为，点B表示的数为，点C表示的数为，

(2)、用含t的代数式表示P到点A和点C的距离：PA＝， PC＝．

(3)、当点P运动到B点时，点Q从A点出发，以每秒点3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A ．
①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．
②在点Q开始运动后，P、Q两点之间的距离能否为4个单位?如果能，请求出此时点P表示的数；如果不能，请说明理由．

查看试题解析

	甲	乙
进价(元/件)	20	30
售价(元/件)	25	40