浙江省杭州市上城区2023-2024学年九年级上学期数学期末模拟试卷
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 将如图的正方形图案绕中心O旋转180°后,得到的图案是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列事件是必然事件的是( )A、通常温度降到 ,纯净的水结冰 B、汽车累计行驶1万千米,从未出现故障 C、姚明在罚球线上投篮一次,投中 D、经过有交通信号灯的路口,遇到绿灯4. 在平面直角坐标系中,如果⊙O是以原点为圆心,以7为半径的圆,那么A(﹣3,4)与⊙O的位置关系是( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定5. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( )
3. 下列事件是必然事件的是( )A、通常温度降到 ,纯净的水结冰 B、汽车累计行驶1万千米,从未出现故障 C、姚明在罚球线上投篮一次,投中 D、经过有交通信号灯的路口,遇到绿灯4. 在平面直角坐标系中,如果⊙O是以原点为圆心,以7为半径的圆,那么A(﹣3,4)与⊙O的位置关系是( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定5. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( ) A、 B、 C、 D、6. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
A、 B、 C、 D、6. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ). A、 B、2 C、 D、7. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( )
A、 B、2 C、 D、7. 如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( ) A、 B、 C、 D、8. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )
A、 B、 C、 D、8. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )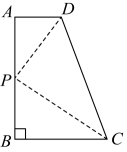 A、0 B、1 C、2 D、39. 如图,在中, , 下列结论中正确的是( )
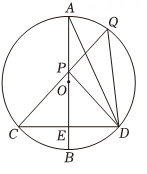
A、0 B、1 C、2 D、39. 如图,在中, , 下列结论中正确的是( ) A、 B、 C、 D、10. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( )
A、 B、 C、 D、10. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( ) A、 B、﹣2 C、﹣2或3 D、﹣6或﹣2
A、 B、﹣2 C、﹣2或3 D、﹣6或﹣2二、填空题(本大题有6个小题,每小题4分,共24分)
-
11. 若线段b是线段a和c的比例中项,且a=1cm,c=9cm,则b=cm.12. 如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为.
 13. 已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则 的值是 .14. 在一个不透明的布袋中,黄色、红色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中红色球的个数很可能是个.15. 已知,点A(1,y1),B(0.5,y2),C(4,y3)都在二次函数y=x24x+c的图象上,则y1 , y2 , y3的大小关系是 .16. 抛物线y=ax2+bx+c(a<0,a、b、c为常数)的部分图象如图所示,其顶点坐标为(-1,n)且与x轴的一个交点在(-3,0)和(-2,0)之间,则下列结论:①a+b+c<0;②2a-b=0;③一元二次方程=0的两根为x1、x2,则|x1-x2|=2;④对于任意实数m , 不等式a(m2-1)+b(m+1)≤0恒成立,其中正确的有(填写序号)
13. 已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则 的值是 .14. 在一个不透明的布袋中,黄色、红色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中红色球的个数很可能是个.15. 已知,点A(1,y1),B(0.5,y2),C(4,y3)都在二次函数y=x24x+c的图象上,则y1 , y2 , y3的大小关系是 .16. 抛物线y=ax2+bx+c(a<0,a、b、c为常数)的部分图象如图所示,其顶点坐标为(-1,n)且与x轴的一个交点在(-3,0)和(-2,0)之间,则下列结论:①a+b+c<0;②2a-b=0;③一元二次方程=0的两根为x1、x2,则|x1-x2|=2;④对于任意实数m , 不等式a(m2-1)+b(m+1)≤0恒成立,其中正确的有(填写序号)
三、解答题(本大题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
17. 计算:(1)、;(2)、若 , 请求出的值.18. 为了解班级学生参加课后服务的学习效果,何老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
 (1)、此次调查的总人数为;(2)、扇形统计图中“不达标”对应的圆心角度数是°;(3)、请将条形统计图补充完整;(4)、为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.19. 已知:如图,在 中, 是 上一点, , 的周长是 cm.
(1)、此次调查的总人数为;(2)、扇形统计图中“不达标”对应的圆心角度数是°;(3)、请将条形统计图补充完整;(4)、为了共同进步,何老师准备从被调查的A类和D类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.19. 已知:如图,在 中, 是 上一点, , 的周长是 cm.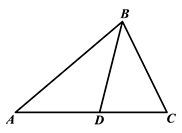 (1)、求 的周长;
(1)、求 的周长;
(2)、求 与 的面积比.
20. 某货站传送货物的平面示意图如图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带 长为 . (1)、求新传送带的长度;(2)、如果需要在货物着地点 的左侧留出 的通道,试判断距离点 处 的货物 是否需要挪走,并说明理由.(说明:(1),(2)的计算结果精确到 ,参考数据: , , , )21. 如图,正方形网格中有一段弧,弧上三点A , B , C均在格点上.
(1)、求新传送带的长度;(2)、如果需要在货物着地点 的左侧留出 的通道,试判断距离点 处 的货物 是否需要挪走,并说明理由.(说明:(1),(2)的计算结果精确到 ,参考数据: , , , )21. 如图,正方形网格中有一段弧,弧上三点A , B , C均在格点上. (1)、请作图找出圆心P的位置,并写出它的坐标.(2)、求的长度.
(1)、请作图找出圆心P的位置,并写出它的坐标.(2)、求的长度.