浙江省宁波北仑区数学2023-2024学年八年级上学期数学期末模拟试卷
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图标,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 若 , 则下列各式正确的是( )A、 B、 C、 D、3. 已知△ABC的三边长都是整数,且AB=2,BC=6,则△ABC的周长可能是( )A、12 B、14 C、16 D、174. 把点P(-x,y)变为Q(x,y),只需( )
2. 若 , 则下列各式正确的是( )A、 B、 C、 D、3. 已知△ABC的三边长都是整数,且AB=2,BC=6,则△ABC的周长可能是( )A、12 B、14 C、16 D、174. 把点P(-x,y)变为Q(x,y),只需( )
A、向左平移2x个单位 B、向右平移2x个单位 C、作关于x轴对称 D、作关于y轴对称5. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( ) A、1 B、1.5 C、2 D、2.56. 点A(3,y1)和点B(-2,y2)都在直线y=-2x+3上,则y1和y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、
A、1 B、1.5 C、2 D、2.56. 点A(3,y1)和点B(-2,y2)都在直线y=-2x+3上,则y1和y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定7. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、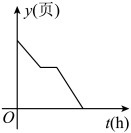 B、
B、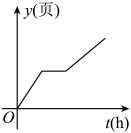 C、
C、 D、
D、 8. 若关于x的不等式组有且仅有2个整数解,则a的取值范围是( )A、3≤a≤4 B、3≤a<4 C、3<a≤4 D、2≤a<49. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )
8. 若关于x的不等式组有且仅有2个整数解,则a的取值范围是( )A、3≤a≤4 B、3≤a<4 C、3<a≤4 D、2≤a<49. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )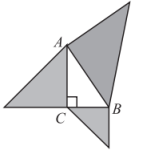 A、6 B、 C、 D、2510. 如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=
A、6 B、 C、 D、2510. 如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=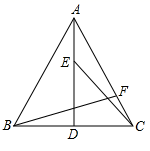 A、112.5° B、105° C、90° D、82.5°
A、112.5° B、105° C、90° D、82.5°二、填空题(本大题有6个小题,每小题4分,共24分)
-
11. 函数中,自变量x的取值范围是12. 命题“如果 ab>0,那么a<0,b<0.”的逆命题是:.13. 在平面直角坐标系中,将直线y=2+4沿向右平移2个单位长后,得到新直线的函数关系式为.14. 若点P在X轴的上方,Y轴的左侧,且到X轴的距离为3,到Y轴的距离为4,则点P的坐标是 .15. 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是 .
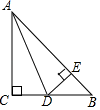 16. 如图,已知是等边三角形,点 , , , 在同一直线上,且 , , 则.
16. 如图,已知是等边三角形,点 , , , 在同一直线上,且 , , 则.
三、解答题(本大题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
17. 已知关于x的不等式组恰好有两个整数解,求实数a的取值范围.18. 如图,在Rt△ABC中,∠ACB=90°
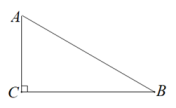 (1)、用直尺和圆规作∠BAC的平分线交BC于点D(保留作图痕迹);(2)、若AD=DB,求∠B的度数.19. 如图所示在正方形网格中,点A的坐标为 , 按要求解答下列问题:
(1)、用直尺和圆规作∠BAC的平分线交BC于点D(保留作图痕迹);(2)、若AD=DB,求∠B的度数.19. 如图所示在正方形网格中,点A的坐标为 , 按要求解答下列问题: (1)、在图中建立正确的平面直角坐标系,并写出点B , C的坐标;(2)、作出三角形ABC关于x轴的对称图形三角形A'B'C'.(不写作法)20. 某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
(1)、在图中建立正确的平面直角坐标系,并写出点B , C的坐标;(2)、作出三角形ABC关于x轴的对称图形三角形A'B'C'.(不写作法)20. 某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,每人一次一张票不限次数.
(1)、分别写出选择普通票、银卡消费时,所需费用 、 与次数 之间的函数表达式;(2)、小明打算暑假每天游泳一次,按55天计算,则选择哪种消费方式更合算?说明理由.21. 已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点. (1)、直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)、直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.22.
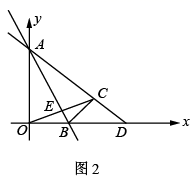
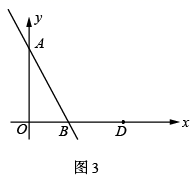
(1)、直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)、直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.22.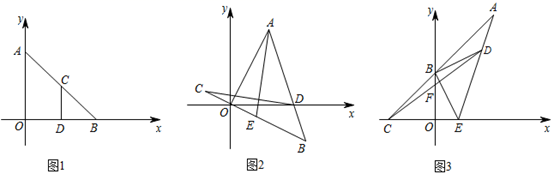 (1)、如图1,平面直角坐标系中A(0,a),B(a,0)(a>0).C为线段AB的中点,CD⊥x轴于D,若△AOB的面积为2,则△CDB的面积为 .(2)、如图2,△AOB为等腰直角三角形,O为直角顶点,点E为线段OB上一点,且OB=3OE,C与E关于原点对称,线段AB交x轴于点D,连CD,若CD⊥AE,试求的值.(3)、如图3,点C、E在x轴上,B在y轴上,OB=OC,△BDE是以B为直角顶点的等腰直角三角形,直线CB、ED交于点A,CD交y轴于点F,试探究:是否为定值?如果是定值,请求出该定值;如果不是,请求出其取值范围.23. 如图1,直线 的解析式为 , 点坐标为 , 点关于直线 的对称点 点在直线 上.
(1)、如图1,平面直角坐标系中A(0,a),B(a,0)(a>0).C为线段AB的中点,CD⊥x轴于D,若△AOB的面积为2,则△CDB的面积为 .(2)、如图2,△AOB为等腰直角三角形,O为直角顶点,点E为线段OB上一点,且OB=3OE,C与E关于原点对称,线段AB交x轴于点D,连CD,若CD⊥AE,试求的值.(3)、如图3,点C、E在x轴上,B在y轴上,OB=OC,△BDE是以B为直角顶点的等腰直角三角形,直线CB、ED交于点A,CD交y轴于点F,试探究:是否为定值?如果是定值,请求出该定值;如果不是,请求出其取值范围.23. 如图1,直线 的解析式为 , 点坐标为 , 点关于直线 的对称点 点在直线 上.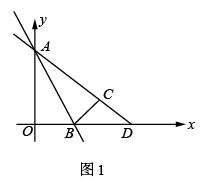
 (1)、求直线 、 的解析式;(2)、如图2,若 交 于点 ,在线段 上是否存在一点 ,使 与 的面积相等,若存在求出 点坐标,若不存在,请说明理由;(3)、如图3,过点 的直线 .当它与直线 夹角等于 时,求出相应 的值.
(1)、求直线 、 的解析式;(2)、如图2,若 交 于点 ,在线段 上是否存在一点 ,使 与 的面积相等,若存在求出 点坐标,若不存在,请说明理由;(3)、如图3,过点 的直线 .当它与直线 夹角等于 时,求出相应 的值.