浙江省嘉兴市桐乡市2023-2024学年八年级上学期数学期末试卷
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(每小题3分,共10题,共30分)
-
1. 下列汽车标志中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点在第四象限,且 , 则点的坐标是( )A、 B、 C、 D、3. 已知 , 下列不等式变形不正确的是( )A、 B、 C、 D、4. 如图,为了估计池塘两岸A , B间的距离,在池塘的一侧选取点 , 测得米,米,那么A , B间的距离不可能是( )
2. 已知点在第四象限,且 , 则点的坐标是( )A、 B、 C、 D、3. 已知 , 下列不等式变形不正确的是( )A、 B、 C、 D、4. 如图,为了估计池塘两岸A , B间的距离,在池塘的一侧选取点 , 测得米,米,那么A , B间的距离不可能是( ) A、6米 B、米 C、27米 D、18米5. 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( )
A、6米 B、米 C、27米 D、18米5. 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( ) A、30° B、45° C、50° D、75°6. 下列命题属于真命题的是( )A、两个角对应相等的两个三角形全等 B、两条边相等的两个直角三角形全等 C、腰相等的两个等腰三角形全等 D、斜边相等的两个等腰直角三角形全等7. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )
A、30° B、45° C、50° D、75°6. 下列命题属于真命题的是( )A、两个角对应相等的两个三角形全等 B、两条边相等的两个直角三角形全等 C、腰相等的两个等腰三角形全等 D、斜边相等的两个等腰直角三角形全等7. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )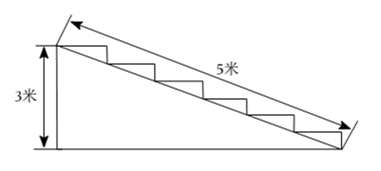 A、米 B、米 C、米 D、米8. 关于函数 , 给出下列说法正确的是:( )
A、米 B、米 C、米 D、米8. 关于函数 , 给出下列说法正确的是:( )①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③9. 如图,已知的平分线与BC的垂直平分线相交于点 , 垂足分别为、 , 则( ) A、6 B、3 C、2 D、1.510. 如图,在△ABC中,∠ABC=45° , BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .
A、6 B、3 C、2 D、1.510. 如图,在△ABC中,∠ABC=45° , BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .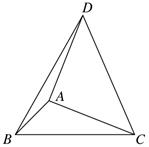 A、8 B、10 C、4 D、8
A、8 B、10 C、4 D、8二、填空题(每小题3分,共6题,共18分)
-
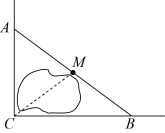
11. 命题“同位角相等,两直线平行”的逆命题是: .12. 如图,公路 , 互相垂直,公路的中点与点被湖隔开,若测得的长为 , 则 , 两点间的距离为 .
 13. 线段CD是由线段AB平移得到的,点的对应点为 , 则点的对应点D的坐标是 .14. 若不等式组无解,则m的取值范围为 .15. 如图,已知一次函数和正比例函数的图象交于点 , 则关于的不等式的解为 .
13. 线段CD是由线段AB平移得到的,点的对应点为 , 则点的对应点D的坐标是 .14. 若不等式组无解,则m的取值范围为 .15. 如图,已知一次函数和正比例函数的图象交于点 , 则关于的不等式的解为 . 16. 在平面直角坐标系中,已知点 , 点是线段上一点,交轴于 , 且 ,
16. 在平面直角坐标系中,已知点 , 点是线段上一点,交轴于 , 且 , (1)、的坐标为: .(2)、若为射线上一点,且 , 则点的坐标为 .
(1)、的坐标为: .(2)、若为射线上一点,且 , 则点的坐标为 .三、解答题(共8题,共52分)
-
17. 解不等式 , 并把解在数轴上表示出来.
 18. 如图,在中.
18. 如图,在中. (1)、作的平分线 .(2)、作线段的垂直平分线.(尺规作图,保留作图痕迹,不写作法)19. 如图,已知直线的图象经过点 , , 且与x轴交于点C .(1)、求直线的解析式;(2)、求的面积.20. 如图,点C , E在上, .
(1)、作的平分线 .(2)、作线段的垂直平分线.(尺规作图,保留作图痕迹,不写作法)19. 如图,已知直线的图象经过点 , , 且与x轴交于点C .(1)、求直线的解析式;(2)、求的面积.20. 如图,点C , E在上, . (1)、求证: .(2)、若 , 求的度数.21. 如图,是等边三角形,点分别在边上,与相交于点 , , 垂足为 .
(1)、求证: .(2)、若 , 求的度数.21. 如图,是等边三角形,点分别在边上,与相交于点 , , 垂足为 . (1)、求的度数.(2)、若 , 求的长.22. 在近期“抗疫”期间,某药店销售A , B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.(1)、求每只A型口罩和B型口罩的销售利润;(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?最大值是多少?
(1)、求的度数.(2)、若 , 求的长.22. 在近期“抗疫”期间,某药店销售A , B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.(1)、求每只A型口罩和B型口罩的销售利润;(2)、该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?最大值是多少?

