浙江省温州市鹿城区2023-2024学年七年级上学期数学期末试卷

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分）

1. 下列结论正确的是（）

A、 $- 2$ 的倒数是2 B、64的平方根是8 C、16的立方根为4 D、算术平方根是本身的数为0和1

查看试题解析
2. 若n为正整数，则计算 ${(- 2)}^{2 n + 1} + 2 \times {(- 2)}^{2 n}$ 的结果是（）

A、0 B、1 C、 $2^{2 n + 1}$ D、 $- 2^{2 n + 1}$

查看试题解析
3. 中国空间站“天宫”的建设引起了全世界的瞩目，其重量约为180000千克，将数据180000用科学记数法表示为（）

A、 $1.8 \times 1 0^{6}$ B、 $18 \times 1 0^{5}$ C、 $1.8 \times 1 0^{5}$ D、 $0.18 \times 1 0^{6}$

查看试题解析
4. 下列说法正确的是（）

A、|-2|与2互为相反数 B、 $\sqrt{3}$ 与 $\frac{1}{\sqrt{3}}$ 互为倒数 C、 $- \sqrt{5} + 1$ ＞ $\frac{\sqrt{3}}{2}$ D、 $\frac{22}{7}$ 是无理数

查看试题解析
5. 关于整式的概念，下列说法正确的是（）

A、 $1$ 是单项式 B、 $5^{2} a^{3} b$ 的次数是 $6$ C、 $- a b^{2} + a b - 6$ 是五次多项式 D、 $\frac{4 π^{3} R}{3}$ 的系数是 $\frac{4}{3}$

查看试题解析
6. 中秋节买月饼，每个梅干菜肉月饼比豆沙月饼多 $2$ 元，购买 $7$ 个梅干菜肉月饼和 $3$ 个豆沙月饼共用 $74$ 元．设每个豆沙月饼 $x$ 元，则可列出方程为（）

A、 $7 x + 3 (x - 2) = 74$ B、 $7 x + 3 (x + 2) = 74$ C、 $7 (x - 2) + 3 x = 74$ D、 $7 (x + 2) + 3 x = 74$

查看试题解析
7. 若关于 $x$ 的方程 $(m - 2) x^{| m | - 1} = 6$ 是一元一次方程，则 $m$ 的值为（）

A、 $\pm 2$ B、-2 C、2 D、4

查看试题解析
8. 已知点A，B，C在同一条直线上，若线段AB＝3，BC＝2，AC＝1，则下列判断正确的是（）

A、点A在线段BC上 B、点B在线段AC上 C、点C在线段AB上 D、点A在线段CB的延长线上

查看试题解析
9. 当x=l时，代数式ax³-3bx+5的值是2019，则当x=-l时，这个代数式的值是（　　）

A、2014 B、-2019 C、2009 D、-2009

查看试题解析
10. 如图，长为 $y$ 、宽为 $x$ 的大长方形被分割为7个小长方形，除阴影 $A$ ， $B$ 外，其余5个是形状、大小完全相同的小长方形，其宽为4．下列说法：①小长方形的长为 $y - 12$ ；②阴影 $A$ 的宽和阴影 $B$ 的宽和为 $x - y + 4$ ；③若 $x$ 为定值，则阴影 $A$ 和阴影 $B$ 的周长为定值．其中正确的是（）

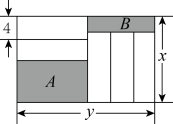A、①③ B、②③ C、①② D、①②③

查看试题解析

二、填空题（6小题，共24分）

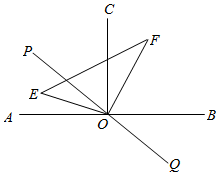
11. $\sqrt{9}$ 的平方根是， -64立方根是.

查看试题解析
12. 若 $3 x^{2} y^{a}$ 与 $- 2 x^{b} y$ 是是同类项，则 $a + b =$

查看试题解析
13. 若 $∠ A = 48 °$ ，则 $∠ A$ 的余角 $=$ °．

查看试题解析
14. 已知 $a - 2 b = 4$ ，则 $3 a + (b - a) - (5 b - 1)$ 的值为．

查看试题解析
15. 当k＝时，关于x的方程 $\frac{1 - k}{4} + 2 x = - \frac{1 - 2 x}{2}$ 的解比关于x的方程 $k (2 + x) = x (k + 2)$ 的解大6

查看试题解析
16. 如图，直线AB⊥OC于点O ， ∠AOP＝40°，三角形EOF其中一个顶点与点O重合，∠EOF＝100°，OE平分∠AOP ，现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E^'OF^' ，同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P^'Q^' ，设运动时间为m秒（0≤m≤20），当直线P^'Q^'平分∠E^'OF^'时，则∠COP^'＝．

查看试题解析

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17.

(1)、计算： $(1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}) \div \frac{7}{8}$ ．

(2)、计算： $\sqrt[3]{- 27} + (3 \sqrt{2} - \sqrt{2}) - \sqrt{2^{2}} + | \sqrt{2} - 3 |$

查看试题解析
18. 解下列方程：

(1)、 $8 x = 6 x - 2 (6 - 4 x)$

(2)、 $\frac{x + 2}{4} - \frac{3 x - 1}{7} = 1$

查看试题解析
19. 化简并求值： $(a - a b) + (b + 2 a b) - (a + b)$ ，其中 $a = \frac{1}{7}$ ， $b = 7$ ．

查看试题解析
20. 某公司要生产若干件新产品，需要精加工后，才能投放市场．现在甲、乙两个加工厂都想加工这批产品，已知甲工厂单独加工这批产品比乙工厂单独加工这批产品多用20天，甲工厂每天可加工16件产品，乙工厂每天可加工24件产品．

(1)、求这个公司要加工新产品的件数．

(2)、在加工过程中，公司需支付甲工厂每天加工费80元，乙工厂每天加工费120元．公司还需另派一名工程师每天到厂家进行技术指导，并负担每天5元的午餐补助费．公司制定产品加工方案如下：可由一个工厂单独加工完成，也可由两个工厂合作同时完成．当两个工厂合作时，这名工程师轮流去这两个工厂．请你通过计算帮助公司从所有可供选择的方案中选择一种既省钱，又省时间的加工方案．

查看试题解析
21. 如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB＝10，动点P从O出发，以每秒6个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．

(1)、写出数轴上点B表示的数；当t＝3时，OP＝；PA＝．

(2)、动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问R运动多少秒时追上点P？

查看试题解析
22. 如图，直线 $A B$ ， $C D$ 相交于点O ， $∠ A O C = 40 °$ ．

(1)、若 $O E ⊥ C D$ ，求 $∠ B O E$ 的度数；

(2)、若 $O A$ 平分 $∠ C O E$ ，求 $∠ D O E$ 的度数．

查看试题解析
23. 某种窗户由上下两部分组成，其上部是用木条围成的半圆形，且半圆形内部由三根等长的木条分隔，下部是用木条围成的边长相等的四个小正方形，木条的宽度和厚度不计．已知下部每个小正方形的边长为a米．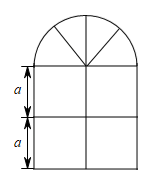

(1)、用含a的代数式分别表示窗户的面积和所用木条的总长度；

(2)、若 $a = 1$ 米，窗户上安装的是玻璃，玻璃25元/平方米，木条20元/米，求制作这个窗户需要的总钱数（ $π$ 值取3，计算结果精确到个位）．

查看试题解析
24. 新定义：从一个角的顶点出发，在角的内部引两条射线，如果这两条射线所成的角等于这个角的一半，那么这两条射线所成的角叫做这个角的内半角．
如图1，若射线 $O C$ 、 $O D$ 在 $∠ A O B$ 的内部，且 $∠ C O D = \frac{1}{2} ∠ A O B$ ，则 $∠ C O D$ 是 $∠ A O B$ 的内半角．
根据以上信息，解决下面的问题：

(1)、如图1， $∠ A O B = 70 ° ， ∠ A O C = 25 °$ ，若 $∠ C O D$ 是 $∠ A O B$ 的内半角，则 $∠ B O D =$ °；

(2)、如图2，已知 $∠ A O B = 60 °$ ，将 $∠ A O B$ 绕点O按顺时针方向旋转一个角度 $α$ （ $0 < α < 60 °$ ）至 $∠ C O D$ ．若 $∠ C O B$ 是 $∠ A O D$ 的内半角，求 $α$ 的值；

(3)、把一块含有30°角的三角板 $C O D$ 按图3方式放置．使 $O C$ 边与 $O A$ 边重合， $O D$ 边与 $O B$ 边重合．如图4，将三角板 $C O D$ 绕顶点O以3度/秒的速度按顺时针方向旋转一周，旋转时间为t秒，当射线 $O A$ 、 $O B$ 、 $O C$ 、 $O D$ 构成内半角时，直接写出t的值．

查看试题解析