湖北省恩施土家族苗族自治州2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题（本大题共有10个小题，每小题3分，共30分在每小题给出的四个选项中，只有一项是符合题目要求的，请将选择项前的字母代号填涂在答题卷相应位置上）

1. 下列手机屏幕手势解锁图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若一个三角形的两边长分别为 $2 c m$ ， $7 c m$ ，则它的第三边的长可能是（）

A、 $2 c m$ B、 $3 c m$ C、 $6 c m$ D、 $9 c m$

查看试题解析
3. 若分式 $\frac{x^{2} - 25}{2 x - 10}$ 的值为零，则x的值是（）

A、5 B、 $- 5$ C、 $\pm 5$ D、0

查看试题解析
4. 下列运算正确的是（）

A、 $3 a^{3} \cdot (- 4 a^{2}) = - 12 a^{5}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 ${(a b^{2})}^{3} = a^{3} b^{5}$ D、 $2 a + 3 b = 5 a b$

查看试题解析
5. 已知关于x的方程 $\frac{4 x - m}{2 x + 4} = 1$ 的解是负数，那么m的取值范围是（）

A、 $m > - 4$ B、 $m < - 4$ C、 $m < - 4$ 且 $m \neq - 8$ D、 $m > - 4$ 且 $m \neq - 8$

查看试题解析
6. 在日常生活中如取款、上网等都需要密码，有一种用“因式分解”法产生的密码记忆方便．原理是：如对于多项式 $x^{4} - y^{4}$ ，因式分解的结果是 $(x - y) (x + y) (x^{2} + y^{2})$ ，若取 $x = 9$ ， $y = 9$ ，则各个因式的值是： $x - y = 0$ ， $x + y = 18$ ， $x^{2} + y^{2} = 162$ ，于是就可以把“018162”作为一个六位数的密码．对于多项式 $x^{3} - x y^{2}$ ，取 $x = 52$ ， $y = 28$ ，用上述方法产生的密码不可能是（）

A、528024 B、522824 C、248052 D、522480

查看试题解析
7. 两个小组同时攀登一座480m高的山，第一组的攀登速度是第二组的1.5倍，第一组比第二组早0.5h到达顶峰，设第二组的攀登速度为vm/min，则下列方程正确的是（）

A、 $\frac{480}{1.5 v} = \frac{480}{v} + 0.5$ B、 $\frac{480}{1.5 v} = \frac{480}{v} - 0.5$ C、 $\frac{480}{1.5 v} = \frac{480}{v} + 30$ D、 $\frac{480}{1.5 v} = \frac{480}{v} - 30$

查看试题解析
8. 如图，已知点D在AC上，点B在AE上， $△ A B C ≅ △ D B E$ ，且∠BDA=∠A，若∠A：∠C=4：3．则∠DBC=（）

A、12° B、24° C、20° D、36°

查看试题解析
9. 如图， $△ A B C$ 中， $∠ A B C = 90 °$ ，点I为 $△ A B C$ 各内角平分线的交点，过I点作 $A C$ 的垂线，垂足为H，若 $B C = 3$ ， $A B = 4$ ， $A C = 5$ ，那么 $I H$ 的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
10. 计算： $(1 - 2 - 3 - \cdot \cdot \cdot - 2023) \times (2 + 3 + \cdot \cdot \cdot + 2024) - (1 - 2 - 3 - \cdot \cdot \cdot - 2024) \times (2 + 3 + \cdot \cdot \cdot + 2023)$ 的值（）

A、2021 B、2022 C、2023 D、2024

查看试题解析

二、填空题（本大题共有5个题，每小题3分，共15分．不要求写出解答过程，请把答案直接填写在答题卷的相应位置上）

11. 等腰三角形的一个角为80°，则这个等腰三角形的顶角的度数为．

查看试题解析
12. 如果 $A (- 1 ， 3)$ ， $B (a ， b - 2)$ 关于x轴对称，则 $a + b =$ ．

查看试题解析
13. 如图，五边形 $A B C D E$ 中， $A E // B C$ ，则 $∠ C + ∠ D + ∠ E$ 的度数为．

查看试题解析
14. 如图，已知 $∠ A B C = 60 °$ ， $D B = 12$ ， $D E = D F$ ，若 $E F = 2$ ，则 $B E =$ ．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3 n$ ， $B C = 4 n$ ， $A B = 5 n$ ， $A D$ 是 $∠ B A C$ 的平分线．若点P，Q分别是 $A D$ 和 $A C$ 上的动点，则 $P C + P Q$ 的最小值是

查看试题解析

三、解答题（本大题共有9个小题，共75分．请在答题卷指定区域内作答，解答时应写出文字说明．证明过程或演算步骤）

16. 计算：

(1)、 $a^{3} \cdot a^{4} \cdot a + {(a^{2})}^{4} + {(- 2 a^{4})}^{2}$

(2)、 $(x + 2 y) (x - y) - {(x + y)}^{2}$

查看试题解析
17. 解分式方程：

(1)、 $\frac{3}{x} - \frac{2}{x + 2} = 0$

(2)、 $\frac{2}{x - 1} + \frac{2 x - 1}{1 - x} = 2$

查看试题解析
18. 先化简，再求值： $(2 a - \frac{12 a}{a + 2}) \div \frac{a - 4}{a^{2} + 4 a + 4}$ ，其中a＝2．

查看试题解析
19. 如图， $A B = D E ， B F = E C ， ∠ B = ∠ E$ ，求证： $A C / / D F$ .

查看试题解析
20. 如图，在△ABC中，AB＝AC ，点D在AC上，且BD＝BC＝AD ，求∠A的度数．

查看试题解析
21. 请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．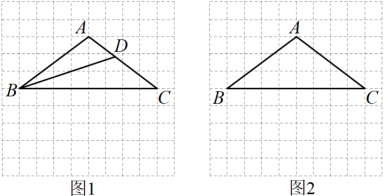
说明：图1、图2中仅点A，B，C在格点上

(1)、在图1中，作 $∠ A$ 的角平分线 $A E$ ；

(2)、在图1中， $B D$ 是 $△ A B C$ 的角平分线，作 $∠ A C B$ 的角平分线 $C F$ ；

(3)、在图2中，画格点H，使 $C H ⊥ A C$ ．

(4)、在图2中，在线段 $B C$ 上画一点G，使 $∠ C A G = 45 °$ ﹒

查看试题解析
22. 某单位为美化环境，计划对面积为1200平方米的区域进行绿化，现安排甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的1.5倍，并且在独立完成面积为360平方米区域的绿化时，甲队比乙队少用 $3$ 天.

(1)、甲、乙两工程队每天能绿化的面积分别是多少平方米？

(2)、若该单位每天需付给甲队的绿化费用为700元，付给乙队的费用为500元，要使这次的绿化总费用不超过14500元，至少安排甲队工作多少天？

查看试题解析
23. 可以利用几何直观的方法获得一些代数结论，如：
例1：如图，可得等式： $a (b + c) = a b + a c$ ；．
例2：如图，可得等式： $(a + 26) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

(1)、如图1，将几个面积不等的小正方形与小长方形拼成一个边长为 $a + b + c$ 的正方形，从中你发现的结论用等式表示为．

(2)、利用（1）中所得到的结论，解决下面的问题：已知 $a + b + c = 10$ ， $a^{2} + b^{2} + c^{2} = 36$ ．求 $a b + b c + a c$ 的值．

(3)、如图2，拼成 $A M G N$ 为大长方形，记长方形 $A B C D$ 的面积与长方形 $E F G H$ 的面积差为S．设 $C D = x$ ，若S的值与 $C D$ 无关，求a与b之间的数量关系．

查看试题解析
24. 已知点A（0，y）在y轴正半轴上，以OA为边作等边△OAB，其中y是方程 $\frac{3}{2 y - 2} + \frac{1}{2} = \frac{3}{y - 1}$ 的解．

(1)、求点A的坐标；

(2)、如图1，点P在x轴正半轴上，以AP为边在第一象限内作等边 $△$ APQ，连QB并延长交x轴于点C，求证OC=BC；

(3)、如图2，若点M为y轴正半轴上一动点，点M在点A的上边，连MB，以MB为边在第一象限内作等边 $△$ MBN，连NA并延长交x轴于点D，当点M运动时，DN−AM的值是否发生变化？若不变，求出其值；若变化，求出其变化的范围．

查看试题解析