湖北省大冶市2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 武汉市元月份某一天早晨的气温是-3℃,中午上升了8℃,则中午的气温是( )A、-5℃ B、5℃ C、3℃ D、-3℃2. 中国财政部表示,为支持进城务工人员随迁子女公平接受义务教育,安排资金亿元.则亿元用科学记数法表示为( )A、元 B、元 C、元 D、元3. 下列图形中,能够折叠成一个正方体的是( )A、
 B、
B、 C、
C、 D、
D、 4. 方程 , ▲处被墨水盖住了,已知方程的解是 , 那么▲处的数字是( )A、 B、 C、4 D、25. 下列每对数中,不相等的一对是( )A、(﹣2)4和﹣24 B、(﹣2)3 和﹣23 C、(﹣2)2和 22 D、|﹣2|3和 236. 下列说法错误的是( )A、2x2-3xy-1是二次三项式 B、-x+1不是单项式 C、-xy2的系数是-1 D、-2ab2是二次单项式7. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β均为锐角且相等的是( )A、
4. 方程 , ▲处被墨水盖住了,已知方程的解是 , 那么▲处的数字是( )A、 B、 C、4 D、25. 下列每对数中,不相等的一对是( )A、(﹣2)4和﹣24 B、(﹣2)3 和﹣23 C、(﹣2)2和 22 D、|﹣2|3和 236. 下列说法错误的是( )A、2x2-3xy-1是二次三项式 B、-x+1不是单项式 C、-xy2的系数是-1 D、-2ab2是二次单项式7. 如图,将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β均为锐角且相等的是( )A、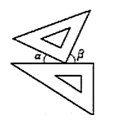 B、
B、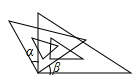 C、
C、 D、
D、 8. 我国唐代有一位尚书杨损任人唯贤,出题选拔官吏.他说:“有人于黄昏时分在林中散步,无意中听到几个盗贼在分赃,偷的大概是布匹,只听得盗贼说,如果每人分6匹,就余5匹;如果每人分7匹,就差8匹,试问有几个盗贼在分多少匹布?”设有x个盗贼,则可以列方程为( )A、 B、 C、 D、9. 卡塔尔卢赛尔体育场是由中国铁建国际集团承建,球场外立面的设计灵感源于阿拉伯吊灯的光影交错的典型图案.该图案是由一些完全相同的小三角形依照规律排列组成,图形(1)由2个小三角形组成,图形(2)由8个小三角形组成,图形(3)由18个小三角形组成,….依次规律,图形(10)由( )个小三角形组成.
8. 我国唐代有一位尚书杨损任人唯贤,出题选拔官吏.他说:“有人于黄昏时分在林中散步,无意中听到几个盗贼在分赃,偷的大概是布匹,只听得盗贼说,如果每人分6匹,就余5匹;如果每人分7匹,就差8匹,试问有几个盗贼在分多少匹布?”设有x个盗贼,则可以列方程为( )A、 B、 C、 D、9. 卡塔尔卢赛尔体育场是由中国铁建国际集团承建,球场外立面的设计灵感源于阿拉伯吊灯的光影交错的典型图案.该图案是由一些完全相同的小三角形依照规律排列组成,图形(1)由2个小三角形组成,图形(2)由8个小三角形组成,图形(3)由18个小三角形组成,….依次规律,图形(10)由( )个小三角形组成. A、100 B、160 C、200 D、30010. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则的值是( )
A、100 B、160 C、200 D、30010. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则的值是( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题(本大题共6小题,每小题3分,共18分)
-
11. ﹣9的相反数是.12. 若与是同类项,则 .13. 已知是锐角,且的余角是它的补角的 , 则 .14. 有理数a,b,c在数轴上的对应位置如图,化简: .
 15. 已知多项式为5次多项式,则 .16. 如图,C为直线上一点,为直角,平分 , 平分 , 平分 , 各学习小组经过讨论后得到以下结论:与互余;;与互补; . 请写出正确结论的序号 .
15. 已知多项式为5次多项式,则 .16. 如图,C为直线上一点,为直角,平分 , 平分 , 平分 , 各学习小组经过讨论后得到以下结论:与互余;;与互补; . 请写出正确结论的序号 .
三、解答题(本大题共8小题,共72分)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、2x+3=﹣3x﹣7;(2)、 .19. 已知多项式与多项式的和为 , 其中.(1)、求多项式.(2)、当取任意值时,式子的值是一个定值,求的值.20. 某种包装盒的形状是长方体,长比高的三倍多2,宽的长度为3分米,它的展开图如图所示.(不考虑包装盒的黏合处)
 (1)、设该包装盒的高为 , 则该长方体的长为分米,边的长度为分米;(用含的式子表示)(2)、若的长为12分米,现对包装盒外表面涂色,每平方分米涂料的价格是6元,求为每个包装盒涂色的费用是多少?(注:包装盒内壁不涂色)21. 已知点C为线段上的一点,点D、E分别为线段中点.(1)、若 , , 求的长;
(1)、设该包装盒的高为 , 则该长方体的长为分米,边的长度为分米;(用含的式子表示)(2)、若的长为12分米,现对包装盒外表面涂色,每平方分米涂料的价格是6元,求为每个包装盒涂色的费用是多少?(注:包装盒内壁不涂色)21. 已知点C为线段上的一点,点D、E分别为线段中点.(1)、若 , , 求的长; (2)、若 , 且点E在点C的右侧,试探究线段与之间的数量关系.
(2)、若 , 且点E在点C的右侧,试探究线段与之间的数量关系. 22. 某社区超市第一次用元购进甲,乙两种商品,其中乙商品的件数比甲商品件数的倍多件,甲、乙两种商品的进价和售价如下表:
22. 某社区超市第一次用元购进甲,乙两种商品,其中乙商品的件数比甲商品件数的倍多件,甲、乙两种商品的进价和售价如下表:甲
乙
进价(元/件)
售价(元/件)
(注:获利=售价-进价)
(1)、该超市第一次购进甲、乙两种商品各多少件?(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?(3)、该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次的总利润多元,求第二次乙商品是按原价打几折销售?23. 对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.例如:数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“联盟点”. (1)、若点A表示数 , 点B表示的数2,下列各数: , 0,1,4,5所对应的点分别为 , 其中是点A,B的“联盟点”的是;(2)、点A表示的数是 , 点B表示的数是3,P是数轴上的一个动点:
(1)、若点A表示数 , 点B表示的数2,下列各数: , 0,1,4,5所对应的点分别为 , 其中是点A,B的“联盟点”的是;(2)、点A表示的数是 , 点B表示的数是3,P是数轴上的一个动点:①若点P在线段上,且点P是点A,B的“联盟点”,求此时点P表示的数:
②若点P在点A的左侧,点P、A、B中有一个点恰好是其它两个点的“联盟点”,求出此时点P表示的数.
24. 如图 (1)、如图1.
(1)、如图1.①若 , 射线OC平分 , 射线OE平分 , 求度数;
②若 , 射线OC平分 , 射线OE平分 , 求的度数;
(2)、如图2,已知 , 射线OQ从射线OA开始,以每秒10°的速度顺时针向射线OD旋转,同时射线OP以每秒20°的速度,从射线OD开始逆时针向射线OA旋转,到达射线OA之后又以同样的角速度顺时针返回,直到到达射线OD时两条射线都停止运动,请问当过了多少秒时,?