湖北省荆州市监利市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、相信你一定能选选对！（本大题共10小题，每小题3分，共30分）

1. 在0，1，﹣3，|﹣3|这四个数中，最小的数是（）

A、0 B、1 C、﹣3 D、|﹣3|

查看试题解析
2. 拒绝“餐桌浪费”，刻不容缓.节约一粒米的帐：一个人一日三餐少浪费一粒米，全国一年就可以节省3240万斤，这些粮食可供9万人吃一年.“3240万”这个数据用科学记数法表示为（）

A、0.324×10⁸ B、32.4×10⁶ C、3.24×10⁷ D、324×10⁸

查看试题解析
3. 下列运算中，正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ C、 $5 a^{2} - 4 a^{2} = 1$ D、 $3 a^{2} b - 3 b a^{2} = 0$

查看试题解析
4. 关于x的方程2x+5a＝3的解与方程2x+2＝0的解相同，则a的值是（）

A、1 B、4 C、 $\frac{1}{5}$ D、﹣1

查看试题解析
5. 如下图几何体是由五个小立方体搭成的，现从左面看它得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
6. 如果 $2 x - y = 3$ ，那么代数式 $4 - 2 x + y$ 的值为（）

A、-1 B、4 C、-4 D、1

查看试题解析
7. 若 $∠ 1$ 与 $∠ 2$ 互为余角， $∠ 1$ 与 $∠ 3$ 互为补角，则下列结论：① $∠ 3 - ∠ 2 = 90 °$ ；② $∠ 3 + ∠ 2 = 270 ° - 2 ∠ 1$ ；③ $∠ 3 - ∠ 1 = 2 ∠ 2$ ；④ $∠ 3 < ∠ 1 + ∠ 2$ ．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 西安某厂车间原计划15小时生产一批急用零件，实际每小时多生产了10个，用了12小时不但完成了任务，而且还多生产了30个.设原计划每小时生产x个零件，则所列方程为（）

A、 $\frac{x}{15} - \frac{x + 30}{12} = 10$ B、 $\frac{x + 30}{12} - \frac{x}{15} = 10$ C、 $12 (x + 10) = 15 x + 30$ D、 $15 x = 12 (x + 10) + 30$

查看试题解析
9. 如图，在数轴上，点A、B表示的数分别是 $- 19$ 和3．点C为线段 $A D$ 的中点，且 $B C = 6 B D$ ，则点C表示的数为（）．

A、 $- 9$ B、 $- 9.5$ C、 $- 10$ D、 $- 10.5$

查看试题解析
10. 如图，将正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到2017个正方形，则需要操作的次数是（）

A、502 B、503 C、504 D、505

查看试题解析

二、你能填得又对又快！（本大题共6小题，每小题3分，共18分）

11. $- \frac{1}{2}$ 的倒数是.

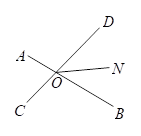
查看试题解析
12. 一个多项式与﹣x²﹣2x+11的和是3x﹣2，则这个多项式为．

查看试题解析
13. 在等式 $3 \times - 2 \times = 15$ 的两个方格中分别填入一个数，使这两个数互为相反数且使等式成立，则第一个方格内的数是.

查看试题解析
14. 如图，已知直线 $A B$ 与 $C D$ 交于点 $O$ ， $O N$ 平分 $∠ D O B$ ，若 $∠ B O C = 110 °$ ，则 $∠ A O N$ 的度数为．

查看试题解析
15. 正方体木块的六个面分别标有数字1，2，3，4，5，6，如图是从不同方向观察这个正方体木块看到的数字情况，数字1和5对面的数字的和是．

查看试题解析
16. 若关于x的方程 $\frac{2 k x + m}{3} = 2 + \frac{x - n k}{6}$ ，无论k为任何数时，它的解总是x＝2，那么m+n＝．

查看试题解析

三、认真解答，一定要细心哟！（本大题共8小题，满分72分）

17. 计算：

(1)、 $12 - (- 18) + (- 7) - 15$

(2)、 $- 2^{3} \div \frac{4}{9} \times {(- \frac{2}{3})}^{2}$

查看试题解析
18. 解方程：

(1)、 $2 (x + 3) - 3 = 7 (x - 1) - 3 x$ ；

(2)、 $\frac{3 y + 1}{2} = \frac{5 y - 1}{3} + 1$

查看试题解析
19.

(1)、先化简，再求值： $2 (a^{2} b + a b^{2}) - 2 (a^{2} b - 1) - a b^{2} - 2$ ，其中 $a = 1$ ， $b = - 3$ ．

(2)、已知平面上三点A、B、C．请按下列要求画出图形：
①画直线 $A B$ ，射线 $B C$ ，线段 $A C$ ；
②过点C画直线 $C D$ ，使 $C D ⊥ A B$ ；
③画出点C到直线 $A B$ 的垂线段 $C E$ ．

查看试题解析
20. 某种包装盒的形状是长方体，长 $A D$ 比高 $A E$ 的三倍多2，宽 $A B$ 的长度为3分米，它的展开图如图所示．（不考虑包装盒的黏合处）

(1)、设该包装盒的高 $A E$ 为 $m$ ，则该长方体的长 $A D$ 为分米，边 $F G$ 的长度为分米；（用含 $m$ 的式子表示）

(2)、若 $F G$ 的长为12分米，现对包装盒外表面涂色，每平方分米涂料的价格是6元，求为每个包装盒涂色的费用是多少？（注：包装盒内壁不涂色）

查看试题解析
21. 将三角尺 $C O D$ 的直角顶点O放置在直线 $A B$ 上．

(1)、按照图1的方式摆放，若 $∠ A O C = 52 °$ ，射线 $O E$ 平分 $∠ B O C$ ，则 $∠ D O E =$ ．

(2)、按照图2的方式摆放，若射线 $O E$ 平分 $∠ B O C$ ，请写出 $∠ A O C$ 与 $∠ D O E$ 之间的数量关系，并说明理由．

查看试题解析
22. 小东同学在解一元一次方程时，发现这样一种特殊现象： $x + \frac{1}{2} = 0$ 的解为 $x = - \frac{1}{2}$ ，而 $- \frac{1}{2} = \frac{1}{2} - 1$ ； $2 x + \frac{4}{3} = 0$ 的解为 $x = - \frac{2}{3}$ ，而 $- \frac{2}{3} = \frac{4}{3} - 2$ ；于是，小东将这种类型的方程作如下定义：若一个关于x的方程ax+b＝0（a≠0）的解为x＝b﹣a，则称之为“奇异方程”.请和小东一起进行以下探究：

(1)、方程 $- 3 x - \frac{9}{2} = 0$ 是“奇异方程”吗？如果是，请说明理由；如果不是，也请说明理由.

(2)、若a＝﹣1，有符合要求的“奇异方程”吗？若有，求出该方程的解；若没有，请说明理由.

(3)、若关于x的方程ax+b＝0（a≠0）为奇异方程，解关于y的方程： $a (a - b) y + 2 = (b + \frac{1}{2}) y$ .

查看试题解析
23. 某社区超市第一次用 $6000$ 元购进甲，乙两种商品，其中乙商品的件数比甲商品件数的 $\frac{1}{2}$ 倍多 $15$ 件，甲、乙两种商品的进价和售价如下表：

甲
乙
进价（元/件）
$22$
$30$
售价（元/件）
$29$
$40$
（注：获利＝售价－进价）

(1)、该超市第一次购进甲、乙两种商品各多少件？

(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(3)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次的总利润多 $180$ 元，求第二次乙商品是按原价打几折销售？

查看试题解析
24. 如图，数轴上点A、C对应的数分别为a、c，且a、c，满足 $| a + 4 | + (c - 1)^{2016} = 0$ ，点O对应的数为0，点B对应的数为 $- 3$ ．

(1)、求数a、c的值；

(2)、点A，B沿数轴同时出发向右匀速运动，点A速度为2个单位长度/秒，点B速度为1个单位长度/秒，几秒后，点A追上点B？

(3)、在（2）的条件下，设运动时间为t秒，在运动过程中，当A，B两点到点C的距离满足 $B C = 2 A C$ 时，求t的值．

查看试题解析

	甲	乙
进价（元/件）	$22$	$30$
售价（元/件）	$29$	$40$