湖北省黄石市大冶市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 汉字是世界上最美的文字,形美如画、有的汉字是轴对称图形,下面四个汉字中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 使分式有意义的条件是( )A、 B、 C、 D、3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )A、 B、 C、 D、4. 下列各式中能用平方差公式的是( )A、(x+y)(y+x) B、(x+y)(y-x) C、(x+y)(-y-x) D、(-x+y)(y-x)5. 下列计算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 已知等腰三角形一边长等于4,另一边长等于10,则它的周长是( )A、17 B、18 C、24 D、18或248. 如图,中,是角平分线,是的中线,若的面积是 , 则的面积是( )
2. 使分式有意义的条件是( )A、 B、 C、 D、3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.0000000076克,将数0.0000000076用科学记数法表示为( )A、 B、 C、 D、4. 下列各式中能用平方差公式的是( )A、(x+y)(y+x) B、(x+y)(y-x) C、(x+y)(-y-x) D、(-x+y)(y-x)5. 下列计算正确的是( )A、 B、 C、 D、6. 如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 已知等腰三角形一边长等于4,另一边长等于10,则它的周长是( )A、17 B、18 C、24 D、18或248. 如图,中,是角平分线,是的中线,若的面积是 , 则的面积是( ) A、5 B、6.8 C、7.5 D、89. 在下面的正方形分割方案中,可以验证的图形是( )A、
A、5 B、6.8 C、7.5 D、89. 在下面的正方形分割方案中,可以验证的图形是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D , ∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( )
10. 如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D , ∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共6小题,每小题3分,共18分)
-
11. 点关于y轴对称的点坐标为 .12. 若 , 则的值是 .13. 已知关于x的分式方程的解为负数,则字母a的取值范围是 .14. 如图,在等边的边长 , 、分别为、的角平分线,、的垂直平分线交于E、F,则的长为 .
 15. 已知 , , 则 . (a、b为正整数)16. 如图,等腰的底边的长为 , 面积是 , 腰的垂直平分线分别交 , 于点E,F,若D为边的中点,M为线段上一动点,则周长的最小值为 .
15. 已知 , , 则 . (a、b为正整数)16. 如图,等腰的底边的长为 , 面积是 , 腰的垂直平分线分别交 , 于点E,F,若D为边的中点,M为线段上一动点,则周长的最小值为 .
三、解答题(本大题共8小题,共72分)
-
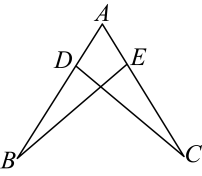
17. 分解因式:(1)、;(2)、 .18. 解分式方程(1)、;(2)、 .19. 先化简,再求值: , 其中 .20. 如图, , 点D、E分别在、上, , 求证: .
 21. 平面直角坐标系的网格中,横、纵坐标均为整数的点叫做格点例如:、都是格点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,要求:保留连线痕迹,不必说明理由.
21. 平面直角坐标系的网格中,横、纵坐标均为整数的点叫做格点例如:、都是格点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,要求:保留连线痕迹,不必说明理由. (1)、在图1中画出一个以为边且与全等的 , 标出点位置;(标出两个点即可)(2)、在图1中画出的中线;(3)、在图2中画出的高线;(4)、在图2中,在y轴正半轴上找一点 , 使 .22. 两个工程队共同参与一项筑路工程,甲队单独施工30天完成总工程的 , 这时增加了乙队,两队又共同工作了15天,完成全部工程.(1)、求乙队单独施工多少天完成全部工程?(2)、若甲队工作4天,乙队工作3天共需支付工程劳务费42000元,甲队工作5天,乙队工作6天共需支付工程劳务费75000元,求甲、乙两队工作一天的劳务费分别为多少元?(3)、在(2)的条件下,若两个工程队不同时施工,在总劳务费不超过28万元的情况下,则最快天能完成总工程.23. 【问题提出】如图1,在中, , D是延长线上的点.连 , 以为边作(E、D在同侧),使 , 连 . 若 , 判断与的位置关系,并说明理由.
(1)、在图1中画出一个以为边且与全等的 , 标出点位置;(标出两个点即可)(2)、在图1中画出的中线;(3)、在图2中画出的高线;(4)、在图2中,在y轴正半轴上找一点 , 使 .22. 两个工程队共同参与一项筑路工程,甲队单独施工30天完成总工程的 , 这时增加了乙队,两队又共同工作了15天,完成全部工程.(1)、求乙队单独施工多少天完成全部工程?(2)、若甲队工作4天,乙队工作3天共需支付工程劳务费42000元,甲队工作5天,乙队工作6天共需支付工程劳务费75000元,求甲、乙两队工作一天的劳务费分别为多少元?(3)、在(2)的条件下,若两个工程队不同时施工,在总劳务费不超过28万元的情况下,则最快天能完成总工程.23. 【问题提出】如图1,在中, , D是延长线上的点.连 , 以为边作(E、D在同侧),使 , 连 . 若 , 判断与的位置关系,并说明理由. (1)、【问题探究】先将问题特殊化.如图2,当D在线段上,时,直接写出的度数;(2)、再探究具体情形、如图1,判断与的位置关系,并说明理由;(3)、如图3,在中, . 点E为外一点,于D, . 求的长.24. 在平面直角坐标系中,点A、B分别在x、y轴上,点、 .
(1)、【问题探究】先将问题特殊化.如图2,当D在线段上,时,直接写出的度数;(2)、再探究具体情形、如图1,判断与的位置关系,并说明理由;(3)、如图3,在中, . 点E为外一点,于D, . 求的长.24. 在平面直角坐标系中,点A、B分别在x、y轴上,点、 . (1)、如图①,若a、b满足 , 判断的形状,并说明理由;(2)、如图②,若即点A不变,点B在y轴正半轴上运动,以为直角边,作等腰直角 , 以为直角边,作等腰直角 , 连接交y轴与Q,当点B在y轴上运动时,试猜想的长是否为定值,若是,请求出来,若不是,说明理由;(3)、如图③,若E点在x轴的正半轴上,且满足 , 于点G,交于点H,探究:的数量关系,并说明理由.
(1)、如图①,若a、b满足 , 判断的形状,并说明理由;(2)、如图②,若即点A不变,点B在y轴正半轴上运动,以为直角边,作等腰直角 , 以为直角边,作等腰直角 , 连接交y轴与Q,当点B在y轴上运动时,试猜想的长是否为定值,若是,请求出来,若不是,说明理由;(3)、如图③,若E点在x轴的正半轴上,且满足 , 于点G,交于点H,探究:的数量关系,并说明理由.