湖北省鄂州市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,满分30分)
-
1. 围棋起源于中国,古代称之为“亦”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算中,正确的是( )A、 B、 C、 D、3. 在下列式子中,属于分式的是( )A、 B、 C、 D、4. 一天课间,小轩同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.如果每块砖的厚度 , 则的长为( )
2. 下列计算中,正确的是( )A、 B、 C、 D、3. 在下列式子中,属于分式的是( )A、 B、 C、 D、4. 一天课间,小轩同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.如果每块砖的厚度 , 则的长为( ) A、100 B、120 C、105 D、1605. 一个正多边形的一个内角等于它的外角的3倍,则这个正多边形是正( )边形.A、四 B、六 C、八 D、十6. 若的展开式中不包含项和项,则( )A、-4 B、3 C、4 D、67. 如图,点是外的一点,点 , 分别是两边上的点,点关于的对称点恰好落在线段上,点关于的对称点落在的延长线上,若 , , , 则线段的长为( )
A、100 B、120 C、105 D、1605. 一个正多边形的一个内角等于它的外角的3倍,则这个正多边形是正( )边形.A、四 B、六 C、八 D、十6. 若的展开式中不包含项和项,则( )A、-4 B、3 C、4 D、67. 如图,点是外的一点,点 , 分别是两边上的点,点关于的对称点恰好落在线段上,点关于的对称点落在的延长线上,若 , , , 则线段的长为( ) A、4 B、5.5 C、6.5 D、78. 定义运算“※”: . 若 , 则的值为( )A、 B、或10 C、10 D、不存在9. 已知等腰 , , 若边上的垂直平分线与直线所夹的锐角为 , 则等腰顶角的度数为( )A、 B、或 C、 D、或10. 如图,射线线段 , 垂足为 , , 垂足为 , , , . 点为射线上的一动点,当的周长最小时,( )
A、4 B、5.5 C、6.5 D、78. 定义运算“※”: . 若 , 则的值为( )A、 B、或10 C、10 D、不存在9. 已知等腰 , , 若边上的垂直平分线与直线所夹的锐角为 , 则等腰顶角的度数为( )A、 B、或 C、 D、或10. 如图,射线线段 , 垂足为 , , 垂足为 , , , . 点为射线上的一动点,当的周长最小时,( ) A、2.5 B、3 C、4 D、4.5
A、2.5 B、3 C、4 D、4.5二、填空题(本题有8小题,每小题3分,共24分)
-
11. 计算: =12. 若分式 的值为0,则x的值为.13. 如图是蜡烛平面镜成像原理图,若以平面为轴,镜面侧面为轴(镜面厚度忽略不计)建立平面直角坐标系,若某时刻火焰顶尖点的坐标是 , 此时对应的虚像的坐标是 , 则 .
 14. 如图,等边的边长为12,点为上一点,于点 , 于点 , 连接 . 若 . 也是等边三角形,则的长 .
14. 如图,等边的边长为12,点为上一点,于点 , 于点 , 连接 . 若 . 也是等边三角形,则的长 . 15. 如图,在中, , 是的一个外角.实验与操作:(1)作的平分线;(2)作线段的垂直平分线,与交于点 , 与边交于点 , 连接 , ;在(1)和(2)的条件下,若 , 则 .
15. 如图,在中, , 是的一个外角.实验与操作:(1)作的平分线;(2)作线段的垂直平分线,与交于点 , 与边交于点 , 连接 , ;在(1)和(2)的条件下,若 , 则 . 16. 已知关于的分式方程的解满足 , 则的取值范围是 .17. 有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:
16. 已知关于的分式方程的解满足 , 则的取值范围是 .17. 有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:
则第次运算的结果 . (用含字母的式子表示)
18. 如图,中, , , . 点从点出发沿路径向终点运动,终点为点;点从点出发沿路径向终点运动,终点为点.点和分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过和作于、作于 , 当点运动秒时,以、、为顶点的三角形和以、、为顶点的三角形全等.
三、解答题(本题有8个小题,共66分,解答要求写出文字说明证明过程或计算步骤)
-
19. 分解因式:(1)、;(2)、 .20. 解分式方程:(1)、;(2)、 .21. 先化简,再求值:
, 其中 .
22. 如图, , , 三点在同一直线上, , , . (1)、求证:;(2)、请你探究:当满足什么条件时, . 并证明它.23. “母亲节”前夕,下冯商店根据市场调查,用3000元购进康乃馨盒装花,上市后很快售完,接着又用4200元购进蓝玫瑰盒装花.已知蓝玫瑰盒装花所购花的盒数是康乃馨盒装花所购花盒数2倍,且蓝玫瑰盒装花每盒花的进价比康乃馨每盒盒装花的进价少3元.(1)、求康乃馨盒装花每盒的进价是多少元?(2)、下冯商店响应习总书记“爱我母亲”的号召,商店决定再次购进康乃馨盒装花和蓝玫瑰盒装花两种盒装花,共1000盒,恰逢花市对这两种盒装花的价格进行调整:康乃馨盒装花每盒进价比第一次每盒进价提高了 , 蓝玫瑰盒装花每盒按第一次每盒进价的9折购进.如果下冯商店此次购买的总费用不超过8000元,那么,下冯商店最少要购买多少盒蓝玫瑰盒装花?24. 在如图所示的的网格中,的三个顶点、、均在格点上.
(1)、求证:;(2)、请你探究:当满足什么条件时, . 并证明它.23. “母亲节”前夕,下冯商店根据市场调查,用3000元购进康乃馨盒装花,上市后很快售完,接着又用4200元购进蓝玫瑰盒装花.已知蓝玫瑰盒装花所购花的盒数是康乃馨盒装花所购花盒数2倍,且蓝玫瑰盒装花每盒花的进价比康乃馨每盒盒装花的进价少3元.(1)、求康乃馨盒装花每盒的进价是多少元?(2)、下冯商店响应习总书记“爱我母亲”的号召,商店决定再次购进康乃馨盒装花和蓝玫瑰盒装花两种盒装花,共1000盒,恰逢花市对这两种盒装花的价格进行调整:康乃馨盒装花每盒进价比第一次每盒进价提高了 , 蓝玫瑰盒装花每盒按第一次每盒进价的9折购进.如果下冯商店此次购买的总费用不超过8000元,那么,下冯商店最少要购买多少盒蓝玫瑰盒装花?24. 在如图所示的的网格中,的三个顶点、、均在格点上. (1)、探究一:如图1,作出关于直线对称的 . (不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);(2)、探究二:如图2,在直线上作一点 , 使的周长最小.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);(3)、探究三:如图3,请尝试运用构造全等三角形法,作出格点边上的高 . (不写作法步骤,仅用无刻度直尺作图,保留作图痕迹)25. 问题情境:
(1)、探究一:如图1,作出关于直线对称的 . (不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);(2)、探究二:如图2,在直线上作一点 , 使的周长最小.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);(3)、探究三:如图3,请尝试运用构造全等三角形法,作出格点边上的高 . (不写作法步骤,仅用无刻度直尺作图,保留作图痕迹)25. 问题情境:定义:如果两个等腰三角形的顶角互补,顶角的顶点又是同一个点,而且这两个等腰三角形的腰也分别相等,则称这两个三角形互为“顶补等腰三角形”.
 (1)、特例证明:
(1)、特例证明:如图1,若与互为“顶补等腰三角形”. , 于 , 于 , 求证:;
(2)、拓展运用:如图2,在四边形中, , , , , 在四边形的内部是否存在点 , 使得与互为“顶补等腰三角形”?若存在,请给予证明;若不存在,请说明理由.
26. 在平面直角坐标系中,点 , , 且 , 满足 .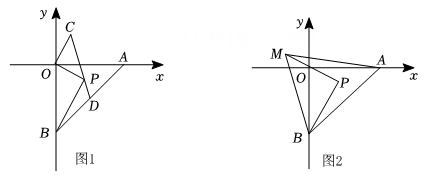 (1)、 , .(2)、连接 , 为内一点, .
(1)、 , .(2)、连接 , 为内一点, .①如图1,过点作 , 且 , 连接 , 并延长交于 . 求证:点为线段的中点;
②如图2,点在的延长线上,连接、 . 若 , 点 , 求: .