湖北省黄石市黄石港区 2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、单选题
-
1. 我市积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式有意义,则的取值范围是( )A、任意实数 B、 C、 D、3. 空气的密度是 0.00129 克每立方厘米,将 0.00129 用科学记数法表示应为( )A、1.29 ×10-3 B、1.29 ×10-5 C、1.29 ×10-4 D、1.29 ×10-24. 下列运算正确的是( )A、 B、 C、 D、5. 在 和 中,已知 , ,添加下列条件中的一个,不能使 一定成立的是( )A、 B、 C、 D、6. 计算的结果为( )A、 B、 C、 D、7. 下列式子从左到右变形是因式分解的是( )A、a2+4a-12=a(a-4)-12 B、a2+4a-12=(a-2)(a+6) C、(a-2)(a+6)=a2+4a-12 D、a2+4a-12=(a+2)2-168. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
2. 若分式有意义,则的取值范围是( )A、任意实数 B、 C、 D、3. 空气的密度是 0.00129 克每立方厘米,将 0.00129 用科学记数法表示应为( )A、1.29 ×10-3 B、1.29 ×10-5 C、1.29 ×10-4 D、1.29 ×10-24. 下列运算正确的是( )A、 B、 C、 D、5. 在 和 中,已知 , ,添加下列条件中的一个,不能使 一定成立的是( )A、 B、 C、 D、6. 计算的结果为( )A、 B、 C、 D、7. 下列式子从左到右变形是因式分解的是( )A、a2+4a-12=a(a-4)-12 B、a2+4a-12=(a-2)(a+6) C、(a-2)(a+6)=a2+4a-12 D、a2+4a-12=(a+2)2-168. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )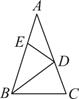 A、2个 B、3个 C、4个 D、5个9. 如图, , 为方格纸中格点上的两点,若以为边,在方格中取一点(在格点上),使得为等腰三角形,则点的个数为( )
A、2个 B、3个 C、4个 D、5个9. 如图, , 为方格纸中格点上的两点,若以为边,在方格中取一点(在格点上),使得为等腰三角形,则点的个数为( )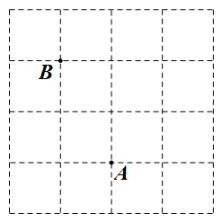 A、 B、 C、 D、10. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( )
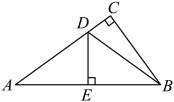
A、 B、 C、 D、10. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( ) A、①③ B、①②④ C、①②③ D、②③
A、①③ B、①②④ C、①②③ D、②③二、填空题
-
11. 若代数式的值为0,则x= .12. 一个正多边形的内角和是 , 则它的一个外角是度.13. 已知是一个完全平方公式,则 .14. 如图,在Rt△ABC中,∠C=90°,DE是线段AB的垂直平分线,已知 , 则∠A= .
 15. 若关于的分式方程无解,则的值为 .16. 如图,在中, , 平分交于D点,E,F分别是 , 上的动点,则的最小值为 .
15. 若关于的分式方程无解,则的值为 .16. 如图,在中, , 平分交于D点,E,F分别是 , 上的动点,则的最小值为 .
三、解答题
-
17.(1)、计算: ;(2)、分解因式: .18. 解方程:(1)、;(2)、 .19. 如图,在中,是边上的中线,是边上一点,延长至点 , 使 , 连结.
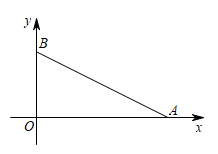
 (1)、求证:.(要求写出每一步的理论依据)(2)、当 , 时,求的度数.20. 先化简,再求值: , 其中 .21. 如图,在平面直角坐标系中, , , .
(1)、求证:.(要求写出每一步的理论依据)(2)、当 , 时,求的度数.20. 先化简,再求值: , 其中 .21. 如图,在平面直角坐标系中, , , .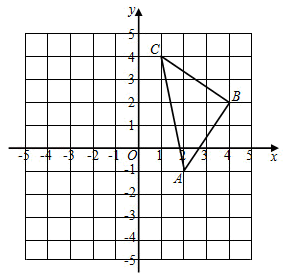 (1)、请画出关于y轴对称的;(2)、直接写出的面积为;(3)、请仅用无刻度的直尺画出的平分线 , 保留作图痕迹.22. 疫情防控形势下,人们在外出时都应戴上口罩以保护自己受新型新冠状病毒感染.某药店用元购进若干包一次性医用口罩,很快售完,该店又用元钱购进第二批这种口罩,所进的包数比第一批多 . 每包口罩的进价比第一批每包口罩的进价多元,请解答下列问题:(1)、求购进的第一批医用口罩有多少包?(2)、政府采取措施,在这两批医用口罩的销售中,售价保持了一致,若售完这两批口罩的总利润不高于元钱,那么药店销售该口罩每包的最高售价是多少元?
(1)、请画出关于y轴对称的;(2)、直接写出的面积为;(3)、请仅用无刻度的直尺画出的平分线 , 保留作图痕迹.22. 疫情防控形势下,人们在外出时都应戴上口罩以保护自己受新型新冠状病毒感染.某药店用元购进若干包一次性医用口罩,很快售完,该店又用元钱购进第二批这种口罩,所进的包数比第一批多 . 每包口罩的进价比第一批每包口罩的进价多元,请解答下列问题:(1)、求购进的第一批医用口罩有多少包?(2)、政府采取措施,在这两批医用口罩的销售中,售价保持了一致,若售完这两批口罩的总利润不高于元钱,那么药店销售该口罩每包的最高售价是多少元?