湖北省黄石市黄石港区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、单选题
-
1. -2的绝对值是( )A、2 B、 C、 D、2. 以学校为观测点,广场在西偏北30°的方向上,如图中正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将去括号,应该等于( )A、 B、 C、 D、4. 一件商品按成本价提高后标价,又以9折销售,这样每卖出一件商品可获利20元.设该商品一件的成本价为元,根据题意,下面所列方程正确的是( ).A、 B、 C、 D、5. 由下面正方体的平面展开图可知,原正方体“我”字所在面的对面的汉字是( )
3. 将去括号,应该等于( )A、 B、 C、 D、4. 一件商品按成本价提高后标价,又以9折销售,这样每卖出一件商品可获利20元.设该商品一件的成本价为元,根据题意,下面所列方程正确的是( ).A、 B、 C、 D、5. 由下面正方体的平面展开图可知,原正方体“我”字所在面的对面的汉字是( ) A、国 B、的 C、中 D、梦6. 已知关于x的方程的解为 , 则m的值等于( )A、2 B、 C、4 D、7. 下列图形中,能用和表示同一个角的是( )A、
A、国 B、的 C、中 D、梦6. 已知关于x的方程的解为 , 则m的值等于( )A、2 B、 C、4 D、7. 下列图形中,能用和表示同一个角的是( )A、
B、
B、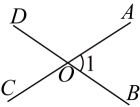
C、
C、
D、
D、
8. 若 , 则等于( )A、 B、 C、 D、9. 已知线段 , 点C是直线上一点, , 点是线段的中点,点N是线段的中点,则线段的长度是( )A、 B、 C、或 D、或10. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有18颗棋子,…,则第⑥个图形中棋子的颗数为( )
8. 若 , 则等于( )A、 B、 C、 D、9. 已知线段 , 点C是直线上一点, , 点是线段的中点,点N是线段的中点,则线段的长度是( )A、 B、 C、或 D、或10. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有18颗棋子,…,则第⑥个图形中棋子的颗数为( ) A、45 B、63 C、84 D、108
A、45 B、63 C、84 D、108二、填空题
-
11. 单项式的系数是 , 次数是 .12. 已知 , 则的补角的度数是 .13. 据科学家估计,地球的年龄大约是4600000000年,这个数用科学记数法表示为.14. 若 , 则 .15. 如图,一副三角板中,将一个三角板角的顶点与另一个三角板的直角顶点重合,如果 , 那么的大小是 度.
 16. 某市近期公布的居民用天然气阶梯价格方案如下:
16. 某市近期公布的居民用天然气阶梯价格方案如下:第一档天然气用量
第二档天然气用量
第三档天然气用量
年用天然气量360立方米及以下,价格为每立方米2元
年用天然气量超出360立方米,不足600立方米时,超过360立方米部分每立方米价格为2.5元.
年用天然气量600立方米以上,超过600立方米部分价格为每立方米3元.
若某户2023年实际缴纳天然气费2463元,则该户2023年使用天然气立方米.
三、解答题
-
17. 计算:(1)、;(2)、 .18. 解方程(1)、(2)、19. 如图,已知三点A、B、C.
 (1)、请读下列语句,并分别画出图形
(1)、请读下列语句,并分别画出图形画直线AB;画射线AC;连接BC.
(2)、在(1)的条件下,图中共有条射线.(3)、从点C到点B的最短路径是 , 依据是.20. 已知:关于的多项式的值与的取值无关.(1)、求的值;(2)、求的值.21. 如图,直线上有一定点O,射线在直线上方,且 . (1)、如图1,当平分时,试证明平分;(2)、如图2,分别作的平分线 , 当时,求的度数;22. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD.
(1)、如图1,当平分时,试证明平分;(2)、如图2,分别作的平分线 , 当时,求的度数;22. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD. (1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.23. 泰州凤城河风景区是国家AAAA景区,景区以望海楼为中心,与桃园、老街交相呼应,吸引各地游客前来旅游观光.其中望海楼和桃园门票零售单价都为40元/人,但团体票单价计算方式不同 .
(1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.23. 泰州凤城河风景区是国家AAAA景区,景区以望海楼为中心,与桃园、老街交相呼应,吸引各地游客前来旅游观光.其中望海楼和桃园门票零售单价都为40元/人,但团体票单价计算方式不同 .望海楼团体票单价计算方式:当旅游团人数不超过25人时,团体票单价为零售单价的90%;当旅游团人数超过25人但不超过50人时,团体票单价为零售单价的85%;当旅游团人数超过50人时,团体票单价为零售单价的80%.
桃园的团体票单价计算方式如下表:
人数范围(人)
0~20
20~40
40~60
60以上
团体票单价(元/人)
零售单价的95%
零售单价的85%
零售单价的70%
零售单价的60%
说明:①0~20是指人数大于0人且小于或等于20人,其他类同;
②桃园团体票单价分段计算 , 与望海楼不同 , 例如,旅游团人数35人,团体票总票价费用为(元).
(1)、若旅游团人数为30人,先后游玩了望海楼和桃园,都购买了团体票,则在望海楼购买门票总费用为元,在桃园购买门票总费用为元;(2)、若旅游团人数为x人( , 即x大于50且小于或等于60),先后游玩了望海楼和桃园,也都购买了团体票,则在望海楼购买门票总费用为元,在桃园购买门票总费用为元(用含x的代数式表示,结果需化简);(3)、若旅游团人数为x人 , 先后游玩了望海楼和桃园,都购买团体票,所付门票总费用是否可能一样?如果可能,求出x的值,如果不可能,请说明理由.24. [阅读材料]数轴是非常重要的数学工具,它可以使问题更加直观.数轴上两点间的距离,可以看作数轴上这两点所对应的数差的绝对值.如图1,数轴上有A、B、C三个点,表示的数分别为:、2、4,A、B两点之间的距离为 .

[初步感知]
(1)、如图1,A、C两点之间的距离为;(2)、数轴上表示x和3两点之间的距离为;(3)、[拓展研究]数轴上有个动点表示的数是x,则的最小值是;
(4)、已知 , 则的最大值是;(5)、[实际应用]某县城可近似看作为一个正方形,如图2,正方形的四个顶点处有四家快递公司A、B、C、 D,它们分别有快递车24辆、12辆、6辆、18辆.为迎接“双十一”活动,使得各快递公司的车辆数相同,允许一些快递公司向相邻公司调动车辆:那么一共调动的车辆数最小值为辆.(不考虑其他因素)
25. 已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段在数轴上移动. (1)、如图1,当线段BC在O、A两点之间移动到某一位置时恰好满足线段 , 求此时b的值;(2)、当线段BC在数轴上沿射线AO方向移动的过程中,若存在 , 求此时满足条件的b值;(3)、当线段BC在数轴上移动时,满足关系式 , 则此时的b的取值范围是 .
(1)、如图1,当线段BC在O、A两点之间移动到某一位置时恰好满足线段 , 求此时b的值;(2)、当线段BC在数轴上沿射线AO方向移动的过程中,若存在 , 求此时满足条件的b值;(3)、当线段BC在数轴上移动时,满足关系式 , 则此时的b的取值范围是 .