湖北省武汉市蔡甸区等3地2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 在①
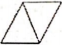 ②
②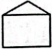 ③
③ ④
④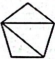 这四个图形中,具有稳定性的有几个?( ) A、1个 B、2个 C、3个 D、4个2. 计算:( )A、 B、 C、 D、3. 使分式有意义的条件是( )A、 B、 C、 D、4. 如图,AC和BD相交于点 , , , 下列说法错误的是( )
这四个图形中,具有稳定性的有几个?( ) A、1个 B、2个 C、3个 D、4个2. 计算:( )A、 B、 C、 D、3. 使分式有意义的条件是( )A、 B、 C、 D、4. 如图,AC和BD相交于点 , , , 下列说法错误的是( ) A、 B、 C、但是 D、且5. 如图,在中, , 是高, , 则( )
A、 B、 C、但是 D、且5. 如图,在中, , 是高, , 则( ) A、3:1 B、3:2 C、4:1 D、2:16. 一个多边形的内角和是它的外角和的6倍,则这个多边形是几边形?( )A、十一边形 B、十二边形 C、十三边形 D、十四边形7. 已知当时,分式无意义;当时,此分式的值为0,则的值是( )A、 B、 C、 D、8. 已知:如图,在中, , . 点在CB的延长线上,且 , 连BE,AC的延长线交BE于点 . 若 , 则( )
A、3:1 B、3:2 C、4:1 D、2:16. 一个多边形的内角和是它的外角和的6倍,则这个多边形是几边形?( )A、十一边形 B、十二边形 C、十三边形 D、十四边形7. 已知当时,分式无意义;当时,此分式的值为0,则的值是( )A、 B、 C、 D、8. 已知:如图,在中, , . 点在CB的延长线上,且 , 连BE,AC的延长线交BE于点 . 若 , 则( ) A、 B、 C、 D、9. 已知 , , 都是正整数,其中 , 且 , 设 , 则( )A、3 B、69 C、3或69 D、2或4610. 如图,是等腰直角三角形,将直角三角形的直角顶点放在BC的中点上,转动 , 设DE,DF分别交AC,BA的延长线于点E,G,连EG,有下列结论:
A、 B、 C、 D、9. 已知 , , 都是正整数,其中 , 且 , 设 , 则( )A、3 B、69 C、3或69 D、2或4610. 如图,是等腰直角三角形,将直角三角形的直角顶点放在BC的中点上,转动 , 设DE,DF分别交AC,BA的延长线于点E,G,连EG,有下列结论:①;②若 , . 则;③;④ , 其中正确的结论有几个?
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(共6小题,每小题3分,共18分)
-
11. 如图, , , 则度.
 12. 计算: .13. 如图,在中,AD是它的角平分线,点是线段AD上的任一点(不与A、重合), , 交BC于点 , , 交BC于点 , 若点到PE的距离为3, , 则
12. 计算: .13. 如图,在中,AD是它的角平分线,点是线段AD上的任一点(不与A、重合), , 交BC于点 , , 交BC于点 , 若点到PE的距离为3, , 则 14. 已知a,b,c是等腰三角形ABC的三边(注:c可能是 , 也可能是),且满足 . 设这个等腰三角形ABC的周长为 , 则15. 在中,与的角平分线交于点 , 边AB和边AC的垂直平分线交于点 , 则与的数量关系是16. 如图,等边在坐标系中如图放置,其顶点的坐标为 , 将沿轴正方向连续翻转(看箭头)若干次,点依次落在点 , , , , …,的位置上,设点的横坐标为 , 则方程的解为
14. 已知a,b,c是等腰三角形ABC的三边(注:c可能是 , 也可能是),且满足 . 设这个等腰三角形ABC的周长为 , 则15. 在中,与的角平分线交于点 , 边AB和边AC的垂直平分线交于点 , 则与的数量关系是16. 如图,等边在坐标系中如图放置,其顶点的坐标为 , 将沿轴正方向连续翻转(看箭头)若干次,点依次落在点 , , , , …,的位置上,设点的横坐标为 , 则方程的解为
三、解答题(共8小题,共72分)
-
17. 计算:(1)、(2)、18. 化简:19. 已知如图, , , , 垂足分别为点 , , ;求证: .
 20. 先化简,再求值:
20. 先化简,再求值:, 其中是方程的解.
21. 如图,在下列带有坐标系的网格图中,△ABC的顶点都在边长为1的小正方形的顶点(我们也把这样的顶点叫做格点)上. (1)、直接写出△ABC的面积 .(2)、画出△ABC关于y轴对称的△DEC(点D与点A对应),直接写出点D的坐标 ▲ .(3)、仅用无刻度的直尺在给定的网格中完成画图.在如图中画出△ABC的高线BF,不写画法,保留作图痕迹.(用虚线表示画图过程,实线表示画图结果).22.(1)、问题背景:两个小组同时开始攀登一座450m高的山,第一组的攀登速度是第二组的1.2倍,他们比第二组早15min到达顶峰,求这两个小组的攀登速度各是多少?(2)、尝试应用:如果山高为hm,第一组的攀登速度是第二组的a倍(其中a>1),并且比第二组早tmin到达顶峰,设第一组的速度为 , 第二组的速度为 .
(1)、直接写出△ABC的面积 .(2)、画出△ABC关于y轴对称的△DEC(点D与点A对应),直接写出点D的坐标 ▲ .(3)、仅用无刻度的直尺在给定的网格中完成画图.在如图中画出△ABC的高线BF,不写画法,保留作图痕迹.(用虚线表示画图过程,实线表示画图结果).22.(1)、问题背景:两个小组同时开始攀登一座450m高的山,第一组的攀登速度是第二组的1.2倍,他们比第二组早15min到达顶峰,求这两个小组的攀登速度各是多少?(2)、尝试应用:如果山高为hm,第一组的攀登速度是第二组的a倍(其中a>1),并且比第二组早tmin到达顶峰,设第一组的速度为 , 第二组的速度为 .①请直接写出 ▲ , ▲ . (结果用含h、a、t的式子表示)
②化简: . (结果用含h、a、t的式子表示)
(3)、拓展应用:在(2)的条件下,设 , , 分解因式:(直接写出结果)23. 如图,在等腰中, , , 点为线段AB上一动点(不与点B重合),且 . (1)、连接BF交AC于点 , 设 .
(1)、连接BF交AC于点 , 设 .①当时,如图1,则 ▲ .
②当时,如图2,若 , 求MC的长.
(2)、如图3,作交CA的延长线于点 , 交BC于点 , 连接PQ,求证: .24. 如图,在平面直角坐标系中,点是轴正半轴上一点,点是轴正半轴上一点,且 , 是多项式中一次项的系数. (1)、直接写出 , 两点的坐标:A( , ),B( , )(2)、如图1,点C为线段OA上一点(点C不与、A重合)且满足: , 连AE,点为轴上一点(点在点的右边),若 , 求证: .(3)、如图2,过点作于点 , 以OB为边在轴左侧作等边 , 连接AQ交OF于点 , 请探究线段PQ、OP、AP三者之间的数量关系并证明你的结论.
(1)、直接写出 , 两点的坐标:A( , ),B( , )(2)、如图1,点C为线段OA上一点(点C不与、A重合)且满足: , 连AE,点为轴上一点(点在点的右边),若 , 求证: .(3)、如图2,过点作于点 , 以OB为边在轴左侧作等边 , 连接AQ交OF于点 , 请探究线段PQ、OP、AP三者之间的数量关系并证明你的结论.