湖北省广水市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、单选题（共30分）

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. 计算 $- 2 - | - 3 |$ 的结果为（）

A、-5 B、-1 C、1 D、5

查看试题解析
3. 已知 $a = b$ ，则下列等式不一定成立的是（）

A、 $a + m = b + m$ B、 $(m - 1) a = (m - 1) b$ C、 $\frac{a}{m^{2}} = \frac{b}{m^{2}}$ D、 $m - a = m - b$

查看试题解析
4. 如图， $C D$ 是直角三角形 $A B C$ 的高，将直角三角形 $A B C$ 按以下方式旋转一周可以得到右侧几何体的是（）．

A、绕着 $A C$ 旋转 B、绕着 $A B$ 旋转 C、绕着 $C D$ 旋转 D、绕着 $B C$ 旋转

查看试题解析
5. 若m，n互为相反数，p，q互为倒数，t的绝对值等于4，则 ${(\frac{m + n}{200})}^{2022} - {(- p q)}^{2023} + t^{3}$ 的值是（）

A、 $- 63$ B、65 C、 $- 63$ 或65 D、63或 $- 65$

查看试题解析
6. 下列说法错误的是（）

A、 $2 x^{2} - 3 x y - 1$ 是二次三项式 B、 $- x + 1$ 不是单项式 C、 $- x y^{2}$ 的系数是 $- 1$ D、 $- 2 a b^{2}$ 是二次单项式

查看试题解析
7. 若多项式 $3 x^{| m |} + (m + 2) x - 7$ 是关于x的二次三项式，则m的值是（）

A、2 B、 $- 2$ C、2或 $- 2$ D、以上答案均不对

查看试题解析
8. 某商人在一次买卖中均以120元卖出两件衣服，一件赚25%，一件赔25%，在这次交易中，该商人( )

A、赚16元 B、赔16元 C、不赚不赔 D、无法确定

查看试题解析
9. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排x名工人生产螺钉，则下面所列方程正确的是（　　）

A、2×1000（26﹣x）=800x B、1000（13﹣x）=800x C、1000（26﹣x）=2×800x D、1000（26﹣x）=800x

查看试题解析
10. 有理数a，b，c在数轴上的位置如图所示：则代数式 $| a + c | - 2 | a - b | + | b - c |$ 化简后的结果为（）

A、b B、 $a - 3 b$ C、 $b + 2 c$ D、 $b - 2 c$

查看试题解析

二、填空题（共18分）

11. 单项式 $\frac{3 a^{2} b}{5}$ 的系数是.

查看试题解析
12. 自中国提出“一带一路·合作共赢”的倡议以来，一大批中外合作项目稳步推进.其中，由中国承建的蒙内铁路（连接肯尼亚首都罗毕和东非第一大港蒙巴萨港），是首条海外中国标准铁路，已于2017年5月31日正式投入运营.该铁路设计运力为25000000吨，将25000000吨用科学记数法表示，记作吨.

查看试题解析
13. 已知 $2 x^{6} y^{2}$ 和 $- x^{3 m} y^{n}$ 是同类项，则 $2 m + n$ 的值是．

查看试题解析
14. 点A，B，C在同一条直线上， $A B = 5 c m ， B C = 2 c m$ ，则 $A C =$ ．

查看试题解析
15. 若要使图中的平面展开图折叠成正方体后，相对面上的两个数之和为6，则 $x + y + z$ 的值为.

查看试题解析
16. 将数字1个1，2个 $\frac{1}{2}$ ，3个 $\frac{1}{3}$ ，4个 $\frac{1}{4}$ …n个 $\frac{1}{n}$ （n为正整数）按顺序排成一排：1， $\frac{1}{2}$ ， $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{3}$ ， $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{4}$ ， $\frac{1}{4}$ ， $\frac{1}{4}$ ，… $\frac{1}{n}$ ， $\frac{1}{n}$ ， $\frac{1}{n}$ …，记a₁=1，a₂= $a_{1} + \frac{1}{2} + \frac{1}{2}$ ，a₃= $a_{2} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3}$ ，…。S₁=a₁ ， S₂=a₁+ a₂ ， S_n= a₁+a₂+a₃+…+ a_n ，则S_1010-S₁₀₀₈=；

查看试题解析

三、解答题（共72分）

17. 计算：

(1)、 $\frac{5}{7} \div (- 2 \frac{2}{5}) - \frac{5}{7} \times \frac{5}{12} - \frac{5}{3} \div 4$

(2)、 ${(- 2)}^{2} \times 5 - {(- 2)}^{3} \div 4 + 3^{2} \times (1 - 3)$

查看试题解析
18. 化简求值： $3 x^{2} - [5 x - (\frac{1}{2} x - 3) + 2 x^{2}]$ ，其中 $x = 4$ ．

查看试题解析
19. 解方程：

(1)、 $2 x - (x + 10) = 5 x + 2 (x - 1)$

(2)、 $\frac{1 - 2 x}{3} = \frac{3 x + 1}{7} - 3$

查看试题解析
20. 如图，已知 $A$ ， $B$ ， $C$ ， $D$ 四点，请按要求作图，并解答．

(1)、画直线 $A B$ ；

(2)、画射线 $D B$ ；

(3)、连接 $A C$ 与射线 $D B$ 交于点 $P$ ；

(4)、若点 $M$ 是线段 $B D$ 的中点， $B P = 3$ ， $D P = 7$ ，求MP的长．

查看试题解析
21. 根据图中情景，解答下列问题：

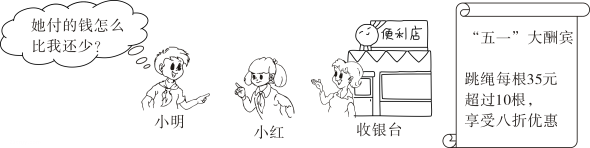(1)、购买8根跳绳需元；购买12根跳绳需元；

(2)、购买m根跳绳需多少元？（请你用含有m的式子表示）

(3)、小红比小明多买2根，付款时小红反而比小明少7元，你认为有这种情况有可能吗？请利用方程知识说明理由．

查看试题解析
22. 如图，已知点C是线段 $A B$ 上一点，点D是线段 $A B$ 的中点，若 $A B = 10 c m$ ， $B C = 3 c m$ ．

(1)、求线段 $C D$ 的长；

(2)、若点E是直线 $A B$ 上一点，且 $B E = 2 c m$ ，点F是 $B E$ 的中点，求线段 $D F$ 的长．

查看试题解析
23. 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为 $1$ 的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将 $0 . \dot{7}$ 化为分数形式．
由于 $0 . \dot{7} = 0.777 ⋯$ ，
设 $x = 0.777 ⋯ ， ⋯ ⋯ ①$
则 $10 x = 7.777 ⋯ ， ⋯ ⋯ ②$
$② - ①$ 得 $9 x = 7$ ，
解得 $x = \frac{7}{9}$ ，于是得 $0 . \dot{7} = \frac{7}{9}$ ．
同理可得 $0 . \dot{3} = \frac{3}{9} = \frac{1}{3}$ ， $1 . \dot{4} = 1 + 0 . \dot{4} = 1 + \frac{4}{9} = \frac{13}{9}$ ．
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

(1)、 $0 . \dot{5} =$ ， $5 . \dot{8} =$ ；

(2)、试比较 $0 . \overset{\cdot}{9}$ 与 $1$ 的大小： $0 . \overset{\cdot}{9}$ $1$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）；

查看试题解析
24. 如图1，点O为直线AB上一点，过O点作射线OC ，使∠AOC：∠BOC=1：3，将一直角△MON的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．绕点O顺时针旋转△MON，其中旋转的角度为α（0<α<360°）.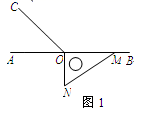

(1)、将图1中的直角△MON旋转至图2的位置，使得ON落在射线OB上，此时α为度；

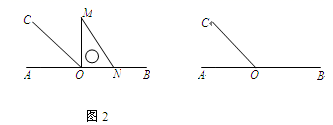(2)、将图1中的直角△MON旋转至图3的位置，使得ON在∠AOC的内部．试探究∠AOM
与∠NOC之间满足什么等量关系，并说明理由；

(3)、在上述直角△MON从图1旋转到图3的位置的过程中，若直角△MON绕点O按每秒25°的速度顺时针旋转，当直角△MON的直角边ON所在直线恰好平分∠AOC时，求此时直角△MON绕点O的运动时间t的值．

查看试题解析