(华师大版)度第二学期七年级数学8.3 一元一次不等式组 同步测试
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
1. 不等式组的解在数轴上表示为( )A、
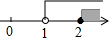 B、
B、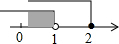 C、
C、 D、
D、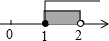 2. 番茄是我们常见的一种蔬菜,取5个大小均等的番茄放在同一简易天平秤,如图,则一个番茄的重量大约是( )
2. 番茄是我们常见的一种蔬菜,取5个大小均等的番茄放在同一简易天平秤,如图,则一个番茄的重量大约是( )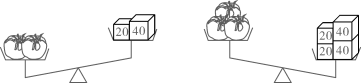 A、30 B、35 C、40 D、453. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、4. 关于的不等式组的最小整数解为1,则的取值范围是( )A、 B、 C、 D、或5. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( )
A、30 B、35 C、40 D、453. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、4. 关于的不等式组的最小整数解为1,则的取值范围是( )A、 B、 C、 D、或5. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( ) A、 B、 C、 D、6. 已知是正数,下列关于的不等式组无解的是( )A、 B、 C、 D、7. 一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、78. 已知关于x的不等式组 , 下列四个结论:
A、 B、 C、 D、6. 已知是正数,下列关于的不等式组无解的是( )A、 B、 C、 D、7. 一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、78. 已知关于x的不等式组 , 下列四个结论:①若它的解集是 , 则;②当 , 不等式组有解;③若它的整数解仅有3个,则a的取值范围是;④若它有解,则 .
其中正确的结论个数( )
A、1个 B、2个 C、3个 D、4个9. 若关于的不等式组的所有整数解的和为 , 则的值不可能是( )A、 B、 C、 D、10. 有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A、x=1,y=3 B、x=3,y=2 C、x=4,y=1 D、x=2,y=3二、填空题
-
11. 若关于的不等式组无解,则的取值范围是 .12. 已知关于的不等式组 , 下列四个结论:
若它的解集是 , 则;
当 , 不等式组有解;
若它的整数解仅有个,则的取值范围是;
若它无解,则 .
其中正确的结论是 填写序号 .13. 若关于的不等式组有解,且关于的方程有非负整数解,则符合条件的所有整数的和为 .14. 已知不等式组的解集是 , 则的值是 .15. 将一箱书分给学生,若每位学生分6本书,则还剩10本书;若每位学生分8本书,则有一个学生分到书但不到4本.求这一箱书的本数与学生的人数.若设有学生x人,则列出的不等式组为 .三、解答题
-
16. 计算:
(1)、;
(2)、把解集在数轴上表示出来 .17. 整式的值为 .(1)、当时,求的值;(2)、若某个关于的不等式的解集如图所示,为该不等式的一个解,求的负整数值; (3)、关于的不等式组恰有两个整数解,求的取值范围.18. 为振兴乡村经济,弘扬“四敢”精神,某村拟建A,B两类展位供当地的农产品展览和销售.1个A类展位的占地面积比1个B类展位的占地面积多4平方米;10个A类展位和5个B类展位的占地面积共 280 平方米.建A类展位每平方米的费用为120元,建B类展位每平方米的费用为100元.(1)、求每个A,B类展位占地面积各为多少平方米?(2)、该村拟建A,B两类展位共40个,B类展位的数量小于A类展位数量的2倍,且建造这40个展位的总费用不超过77000元,求该村共有哪些建设方案?19. 我学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.(1)、甲、乙两种书柜每个的价格分别是多少元?(2)、若我校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你给出费用最省的方案,并求出该方案所需费用.20. 中医药是中华民族的宝贵财富.为更好地弘扬中医药传统文化,传播中医药知识,增进青少年对中华优秀传统文化的了解与认知.明德麓谷学校开展“中草药种植进校园 传承中医药文化”活动,特开设中草药种植课程,计划购买甲、乙两种中草药种子,经过调查得知:每斤甲种种子的价格比每斤乙种种子的价格贵40元,买5斤甲种种子和10斤乙种种子共用1100元.(1)、求每斤甲、乙种子的价格分别是多少元?(2)、若学校需购进乙种中草药种子m斤(其中m为整数),且甲、乙两种中草药种子共120斤,总费用低于8500元,并且要求购进乙种的数量必须不超过甲种数量的3倍,问有几种购买方案?最低费用是多少?
(3)、关于的不等式组恰有两个整数解,求的取值范围.18. 为振兴乡村经济,弘扬“四敢”精神,某村拟建A,B两类展位供当地的农产品展览和销售.1个A类展位的占地面积比1个B类展位的占地面积多4平方米;10个A类展位和5个B类展位的占地面积共 280 平方米.建A类展位每平方米的费用为120元,建B类展位每平方米的费用为100元.(1)、求每个A,B类展位占地面积各为多少平方米?(2)、该村拟建A,B两类展位共40个,B类展位的数量小于A类展位数量的2倍,且建造这40个展位的总费用不超过77000元,求该村共有哪些建设方案?19. 我学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.(1)、甲、乙两种书柜每个的价格分别是多少元?(2)、若我校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你给出费用最省的方案,并求出该方案所需费用.20. 中医药是中华民族的宝贵财富.为更好地弘扬中医药传统文化,传播中医药知识,增进青少年对中华优秀传统文化的了解与认知.明德麓谷学校开展“中草药种植进校园 传承中医药文化”活动,特开设中草药种植课程,计划购买甲、乙两种中草药种子,经过调查得知:每斤甲种种子的价格比每斤乙种种子的价格贵40元,买5斤甲种种子和10斤乙种种子共用1100元.(1)、求每斤甲、乙种子的价格分别是多少元?(2)、若学校需购进乙种中草药种子m斤(其中m为整数),且甲、乙两种中草药种子共120斤,总费用低于8500元,并且要求购进乙种的数量必须不超过甲种数量的3倍,问有几种购买方案?最低费用是多少?