（华师大版）2023-2024学年度第二学期七年级数学7.4 实践与探索同步测试

试卷更新日期：2024-02-21 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在长为30m、宽为20m的长方形公园里，原有两条面积相等的小路，其余部分为绿地.现在为了增加绿地面积，把公园里的一条小路改为绿地，只保留另一条小路，并且使得绿地面积是小路面积的4倍，则x与y的值分别为（）

A、 $\{\begin{matrix} x = 3 ， \\ y = 2 \end{matrix}$ B、 $\{\begin{matrix} x = 5 ， \\ y = 4 \end{matrix}$ C、 $\{\begin{matrix} x = 6 ， \\ y = 5 \end{matrix}$ D、 $\{\begin{matrix} x = 6 ， \\ y = 4 \end{matrix}$

查看试题解析
2. 一个两位数，个位上的数字与十位上的数字之和为7，如果这个两位数加上45恰好成为个位数字与十位数字对调后组成的新两位数，那么原来的两位数为（）

A、61 B、16 C、52 D、25

查看试题解析
3. 利用两块长方体木块测量一张桌子的高度．首先按图1的方式放置，再交换两木块的位置，按图2的方式放置．测量的数据如图所示，则桌子的高度是（）

A、73cm B、74cm C、75cm D、76cm

查看试题解析
4. 根据图中提供的信息，可知每个杯子的价格是(　　)

A、51元 B、35元 C、8元 D、7.5元

查看试题解析
5. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元．求有几个人及该物品的价格．设有x人，该物品价格为y元/件，依题意得（）

A、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$ B、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ C、 ${\begin{array}{l} \frac{y}{8} - 3 = x \\ \frac{y}{7} + 4 = x \end{array}$ D、 ${\begin{array}{l} \frac{y}{8} + 3 = x \\ \frac{y}{7} - 4 = x \end{array}$

查看试题解析
6. 如图，七个相同的小长方形组成一个大长方形 $A B C D$ ，若 $C D = 21$ ，则长方形 $A B C D$ 的面积为（）

A、540 B、630 C、210 D、102

查看试题解析
7. 甲、乙两人相距42km，若同时相向而行，2h后相遇；若同时同向而行，乙14h后才能追上甲，则甲、乙两人每小时各行（）

A、9km，12km B、10km，11km C、101km，101km D、101km，110km

查看试题解析
8. 如图，在数轴上，点 $A$ 、 $B$ 分别表示数 $a$ 、 $b$ ，且 $a + b = 0$ .若 $A B = 4$ ，则点 $A$ 表示的数为（）

A、 $- 4$ B、 $- 2$ C、2 D、4

查看试题解析
9. 游泳池中有一群小朋友，男孩戴蓝色泳帽，女孩戴红色泳帽．每位男孩看到蓝色泳帽比红色泳帽多7顶，而每位女孩看到的蓝色泳帽比红色泳帽多一倍．若设男孩有x人，女孩有y人，则可列方程组（）

A、 ${\begin{cases} x = y + 7 \\ x = 2 y \end{cases}$ B、 ${\begin{cases} x - 1 = y + 7 \\ x = 2 y \end{cases}$ C、 ${\begin{cases} x - 1 = y + 7 \\ x = 2 (y - 1) \end{cases}$ D、 ${\begin{cases} x + 1 = y + 7 \\ x = 2 (y + 1) \end{cases}$

查看试题解析
10. 甲、乙两人练习跑步，若乙先跑10米，则甲跑5秒就可以追上乙；若乙先跑2秒，则甲跑4秒就可以追上乙．若设甲的速度为每秒x米，乙的速度为每秒y米，则下列方程组中正确的是（）

A、 ${\begin{cases} 5 x = 5 y + 10 \\ 4 x = 4 y + 2 y \end{cases}$ B、 ${\begin{cases} 5 x - 5 y = 10 \\ 4 x + 2 y = 4 y \end{cases}$ C、 ${\begin{cases} 5 x + 10 = 5 y \\ 4 x - 4 y = 2 \end{cases}$ D、 ${\begin{cases} 5 x - 5 y = 10 \\ 4 x - 2 = 4 y \end{cases}$

查看试题解析

二、填空题

11. 某眼镜厂有工人25名，每人每天平均生产镜架9个或镜片12片.为了使每天生产的镜架和镜片刚好配套，设x名工人生产镜架，y名工人生产镜片，则可列出方程组：.

查看试题解析
12. 已知关于x，y的二元一次方程组 $\{\begin{matrix} x + 2 y = - a + 1 ， \\ x - 3 y = 4 a + 6 \end{matrix}$ （a是常数)，若不论a取什么实数，代数式kx-y(k是常数)的值始终不变，则k的值为.

查看试题解析
13. 在长方形ABCD中，放入六个形状、大小相同的小长方形，所标尺寸如图所示，则图中阴影部分的面积为cm².

查看试题解析
14. 打折前，买50件A 商品和30 件 B 商品用了 920元，买60件A商品和10件B商品用了1000元.打折后，买 400件 A 商品和400 件 B 商品用了7500元，比打折前少花了元.

查看试题解析
15. 师生对话，师：我像你这么大的时候，你才1岁，你到我这么大的时候，我已经40岁了.老师现在的年龄是.

查看试题解析

三、解答题

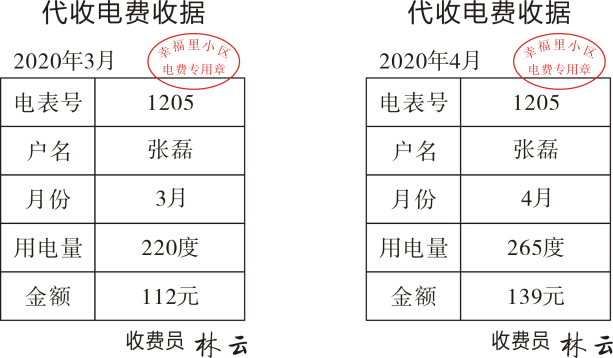
16. 为了确保安全，信息在传输时往往需要加密.当发送方发出一组密码a，b，c时，接收方对应收到的密码为 A，B，C.双方约定：A=2a-b，B=2b，C=b+c，例如：发出1，2，3，则收到0，4，5，

(1)、当发送方发出一组密码为2，3，5时，接收方收到的密码是多少？

(2)、当接收方收到一组密码为2，8，11时，发送方发出的密码是多少？

查看试题解析
17. 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费"(总电费=第-阶梯电费+第二阶梯电费)，规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费．以下是张磊家2020年3月和4月所交电费的收据，问该市规定的第一阶梯电价和第二阶梯电价分别为每度多少元？

查看试题解析
18. 小张在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形，如图1；小红拼成了如图2那样的正方形，中间还留下了一个洞，恰好是边长为3cm的小正方形，求每个小长方形的面积．

查看试题解析
19. 某景点的门票价格如下表所示：
购票人数(人)
1~50
51~100
100以上
每人门票(元)
12
10
8
某校七年级(1)，(2)两班计划去游览该景点，两班总人数之和多于100人，其中(1)班人数少于50人，(2)班人数多于50人且少于100人．若两班都以班为单位单独购票，则一共需支付1118元；若两班联合起来作为一个团体购票，则只需花费816元．

(1)、问：两个班各有多少名学生？

(2)、团体购票与单独购票相比较，两个班各节约了多少元？

查看试题解析
20. 某品牌童装专卖店新推出 A，B，C三种款式的春装.某个周末的销售量（单位：件）如（下表：)

A
B
C
合计
周六的销售量

y

30
周日的销售量
x
2y
4x
5x+2y
合计
10
3y

30+5x+2y

(1)、请根据表格信息，补全表格中的划线部分（用含 x，y的代数式表示）.

(2)、已知A 款周六的销售量与 B 款周日的销售量相等，且这个周末C款的销售总量比A，B 两款的销售总量之和还多 4件.
①求x，y的值.
②已知三种款式的春装单价均为大于 100 的整数，且 A 款的单价是 B 款的 3 倍.如果周六的总销售额为 5 600元，那么B款的单价可以是（写出所有可能的结果）.

查看试题解析

	A	B	C	合计
周六的销售量		y		30
周日的销售量	x	2y	4x	5x+2y
合计	10	3y		30+5x+2y

购票人数(人)	1~50	51~100	100以上
每人门票(元)	12	10	8

（华师大版）2023-2024学年度第二学期七年级数学7.4 实践与探索 同步测试

一、选择题

二、填空题

三、解答题

（华师大版）2023-2024学年度第二学期七年级数学7.4 实践与探索同步测试