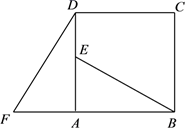2024年北师大版数学八年级下册周测卷(第三章第3-4节)培优卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 生活中有许多对称美的图形,下列是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列命题:①各边相等的多边形是正多边形;②正多边形是中心对称图形;③正六边形的外接圆半径与边长相等;④正n边形共有n条对称轴.其中真命题的个数是( )A、4 B、3 C、2 D、13. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、
2. 下列命题:①各边相等的多边形是正多边形;②正多边形是中心对称图形;③正六边形的外接圆半径与边长相等;④正n边形共有n条对称轴.其中真命题的个数是( )A、4 B、3 C、2 D、13. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,是中心对称图形的是( )A、
4. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 观察如图所示的几何体,下列关于其三视图的说法正确的是( )
5. 观察如图所示的几何体,下列关于其三视图的说法正确的是( ) A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形6. 下面图形中既是轴对称图形又是中心对称图形的是( )
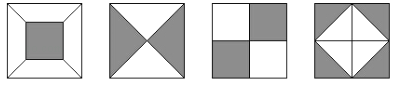
A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形6. 下面图形中既是轴对称图形又是中心对称图形的是( ) A、科克曲线 B、笛卡尔心形线 C、阿基米德螺旋线 D、赵爽弦图7. 如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
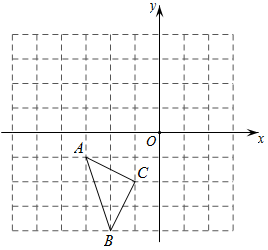
A、科克曲线 B、笛卡尔心形线 C、阿基米德螺旋线 D、赵爽弦图7. 如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( ) A、主视图 B、左视图 C、俯视图 D、不存在8. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )
A、主视图 B、左视图 C、俯视图 D、不存在8. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )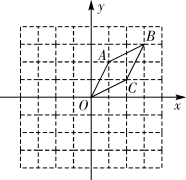 A、 B、 C、 D、9.
A、 B、 C、 D、9.下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )
 A、4个 B、3个 C、2个 D、1个10. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )
A、4个 B、3个 C、2个 D、1个10. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )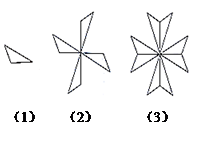 A、轴对称 B、旋转 C、中心对称 D、平移
A、轴对称 B、旋转 C、中心对称 D、平移二、填空题(每题3分,共18分)
-
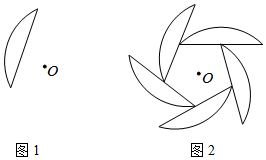
11. 利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α , 则α至少为 .
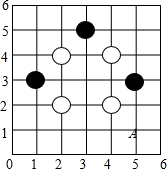
 12. 已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为。13. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)
12. 已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为。13. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3)
 14. 如图,在平面直角坐标系xOy中,△OCD可以看作是△ABO经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABO得到△OCD的过程:.
14. 如图,在平面直角坐标系xOy中,△OCD可以看作是△ABO经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABO得到△OCD的过程:.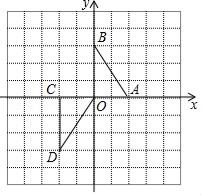 15. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)
15. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)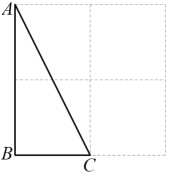 16. 如图,△ABC和△DEF关于点O成中心对称,要得到△DEF , 需要将△ABC绕点O旋转角是
16. 如图,△ABC和△DEF关于点O成中心对称,要得到△DEF , 需要将△ABC绕点O旋转角是
三、解答题(共8题,共72分)
-
17. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
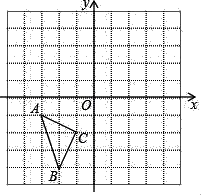 (1)、以O为中心作出△ABC的中心对称图形△A1B1C1 , 并写出点B1坐标;(2)、以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.18. 如图,图①、图②均为6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A,B,C均为格点,只用无刻度的直尺,在给定的网格中按要求画图.
(1)、以O为中心作出△ABC的中心对称图形△A1B1C1 , 并写出点B1坐标;(2)、以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.18. 如图,图①、图②均为6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A,B,C均为格点,只用无刻度的直尺,在给定的网格中按要求画图. (1)、在图①中,画出关于点C中心对称点的图形;(2)、在图②中,将绕点C逆时针旋转90°后得到 , 画出 .19.(1)、观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征: , .
(1)、在图①中,画出关于点C中心对称点的图形;(2)、在图②中,将绕点C逆时针旋转90°后得到 , 画出 .19.(1)、观察分析:在一次数学综合实践活动中,老师向同学们展示了图①,图②,图③三幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出三个图案都具有的两个共同特征: , . (2)、动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征.
(2)、动手操作:请在图④中设计一个新的图案,使其满足你在(1)中发现的共同特征. 20. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
20. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)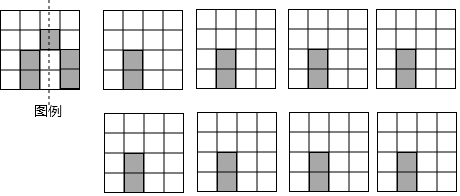 21. 如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连结AE并延长,与BC的延长线交于点F.
21. 如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连结AE并延长,与BC的延长线交于点F. (1)、E是线段CD的 , 点A 与点F关于点成中心对称;(2)、若AB=AD+BC ,求证:△ABF是等腰三角形;(3)、四边形ABCD的面积为12,求△ABF的面积22. 阅读材料,并回答下列问题:
(1)、E是线段CD的 , 点A 与点F关于点成中心对称;(2)、若AB=AD+BC ,求证:△ABF是等腰三角形;(3)、四边形ABCD的面积为12,求△ABF的面积22. 阅读材料,并回答下列问题:如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
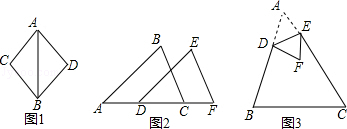 (1)、请你写出一种全等变换的方法(除翻折、平移外).;(2)、如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC=;(3)、如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .
(1)、请你写出一种全等变换的方法(除翻折、平移外).;(2)、如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC=;(3)、如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .