2024年北师大版数学八年级下册周测卷(第三章第1-2节)培优卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,将线段先向左平移,使点B与原点O重合,再将所得线段绕原点旋转得到线段 , 则点A的对应点的坐标是( )
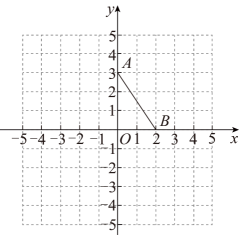 A、 B、 C、 D、2. 如图,已知点 , , 若将线段平移至 , 其中点 , , 则的值为( )
A、 B、 C、 D、2. 如图,已知点 , , 若将线段平移至 , 其中点 , , 则的值为( )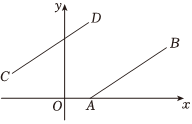 A、 B、 C、 D、3. 如图,用平移方法说明平行四边形的面积公式时,若平移到 , , , 则的平移距离为( )
A、 B、 C、 D、3. 如图,用平移方法说明平行四边形的面积公式时,若平移到 , , , 则的平移距离为( )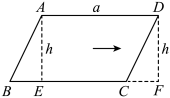 A、3 B、4 C、5 D、124. 如图,在直角坐标系中,各点坐标分别为 , , . 先作关于x轴成轴对称的 , 再把平移后得到 . 若 , 则点坐标为( )
A、3 B、4 C、5 D、124. 如图,在直角坐标系中,各点坐标分别为 , , . 先作关于x轴成轴对称的 , 再把平移后得到 . 若 , 则点坐标为( ) A、 B、 C、 D、5. 如图,将沿向右平移得到 , 若 , , 则的长是( )
A、 B、 C、 D、5. 如图,将沿向右平移得到 , 若 , , 则的长是( ) A、2 B、 C、3 D、56. 如图,在平面直角坐标系中,已知点 , 点 , 以点P为中心,把点A按逆时针方向旋转得到点B,在 , , , 四个点中,直线经过的点是( )
A、2 B、 C、3 D、56. 如图,在平面直角坐标系中,已知点 , 点 , 以点P为中心,把点A按逆时针方向旋转得到点B,在 , , , 四个点中,直线经过的点是( )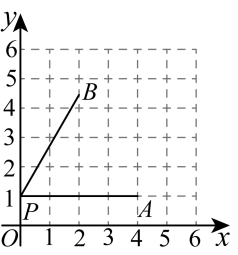 A、 B、 C、 D、7. 如图,将绕点A逆时针旋转到 , 旋转角为 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数为( )
A、 B、 C、 D、7. 如图,将绕点A逆时针旋转到 , 旋转角为 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数为( )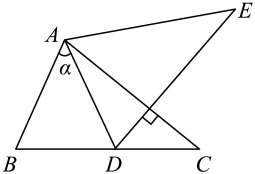 A、 B、 C、 D、8. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A、 B、 C、 D、8. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( ) A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)9. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )
A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)9. 如图,把以点A为中心逆时针旋转得到 , 点B,C的对应点分别是点D,E,且点E在的延长线上,连接 , 则下列结论一定正确的是( )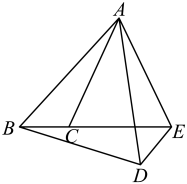 A、 B、 C、 D、10. 如图, 的三个顶点都在方格纸的格点上,其中 点的坐标是 ,现将 绕 点按逆时针方向旋转 ,则旋转后点 的坐标是( )
A、 B、 C、 D、10. 如图, 的三个顶点都在方格纸的格点上,其中 点的坐标是 ,现将 绕 点按逆时针方向旋转 ,则旋转后点 的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
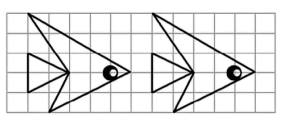
11. 在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是 .
 12. 在平面直角坐标系中,将点向左平移5个单位长度,得到点 , 则点的坐标是 .13. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
12. 在平面直角坐标系中,将点向左平移5个单位长度,得到点 , 则点的坐标是 .13. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .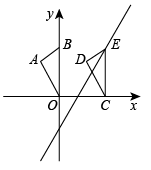 14. 如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为.
14. 如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为. 15. 在直角坐标系中,点(4,5)绕原点O逆时针方向旋转90°,得到的点的坐标是.16. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
15. 在直角坐标系中,点(4,5)绕原点O逆时针方向旋转90°,得到的点的坐标是.16. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .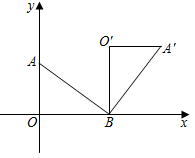
三、解答题(共8题,共72分)
-
17. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连结BE.
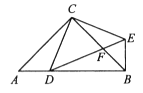 (1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数.18. 如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数.18. 如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.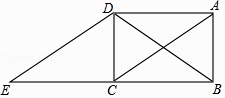 (1)、求证:△ACD≌△EDC;(2)、请探究△BDE的形状,并说明理由.19. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上.
(1)、求证:△ACD≌△EDC;(2)、请探究△BDE的形状,并说明理由.19. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上. (1)、求证:AE平分;(2)、连接BD,求证: .20.
(1)、求证:AE平分;(2)、连接BD,求证: .20.如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△A1B1C1向下平移3个单位,画出平移后的△A2B2C2;
(3)将△A2B2C2绕点C2顺时针旋转90°,画出旋转后的△A3B3C2;并直接写出点A3、B3的坐标.
 21. 如图,在平面直角坐标系中,的三个顶点坐标分别是 , , .
21. 如图,在平面直角坐标系中,的三个顶点坐标分别是 , , .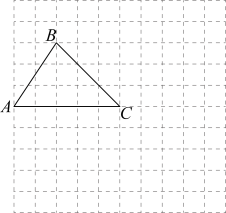 (1)、请在图中画出这个平面直角坐标系;(2)、点经过平移后的对应点为 , 将作同样的平移得到 , 使点的对应点为点 , 点的对应点为点 , 请写出点 , 点的坐标并在图中画出平移后的;(3)、在(2)的条件下,点在直线上,若 , 直接写出点的坐标.22. 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示.
(1)、请在图中画出这个平面直角坐标系;(2)、点经过平移后的对应点为 , 将作同样的平移得到 , 使点的对应点为点 , 点的对应点为点 , 请写出点 , 点的坐标并在图中画出平移后的;(3)、在(2)的条件下,点在直线上,若 , 直接写出点的坐标.22. 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示.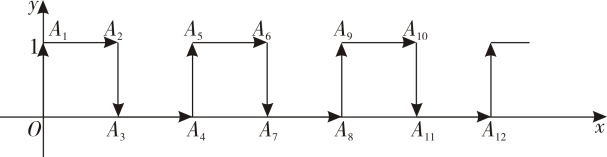 (1)、填写下列各点的坐标:A₁( , )、A₃( , )、A₁₂( , );(2)、写出点A₄n的坐标(n是正整数);(3)、指出蚂蚁从点A₁₀₀到点A₁₀₁的移动方向.23. 如图,点O在直线上, . 在中, , . 先将的一边与重合,然后绕点O顺时针方向旋转,当与重合时停止旋转.
(1)、填写下列各点的坐标:A₁( , )、A₃( , )、A₁₂( , );(2)、写出点A₄n的坐标(n是正整数);(3)、指出蚂蚁从点A₁₀₀到点A₁₀₁的移动方向.23. 如图,点O在直线上, . 在中, , . 先将的一边与重合,然后绕点O顺时针方向旋转,当与重合时停止旋转. (1)、如图①,当在与之间,且时,则度,度.(2)、如图②,当在与之间时,求与差的度数.(3)、在旋转的过程中,若 , 求旋转角的度数.24. 在数学活动课中,同学们用一副直角三角板(分别记为三角形和三角形 , 其中 , , , , 且)开展数学活动.
(1)、如图①,当在与之间,且时,则度,度.(2)、如图②,当在与之间时,求与差的度数.(3)、在旋转的过程中,若 , 求旋转角的度数.24. 在数学活动课中,同学们用一副直角三角板(分别记为三角形和三角形 , 其中 , , , , 且)开展数学活动.
操作发现:
(1)、如图1,将三角形沿方向移动,得到三角形 , 我们会发现 , 推理的根据是:;(2)、将这副三角板如图2摆放,并过点E作直线a平行于边所在的直线b,点A与点F重合,求的度数;(3)、在(2)的条件下,如图3,固定三角形 , 将三角形能点C旋转一周,当时,请判断直线和直线b是否垂直,并说明理由.