2024年北师大版数学八年级下册周测卷（第三章第1-2节）基础卷

试卷更新日期：2024-02-21 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，平面直角坐标系中，线段 $A B$ 的两端点坐标分别为 $(0 ， 2)$ ， $(- 2 ， 0)$ ，现将该线段沿 $x$ 轴向右平移，使得点 $B$ 与原点重合，得到线段 $C O$ ，则点 $C$ 的坐标是（）

A、 $(2 ， 0)$ B、 $(2 ， 2)$ C、 $(\sqrt{2} ， \sqrt{2})$ D、 $(\sqrt{2} ， 2)$

查看试题解析
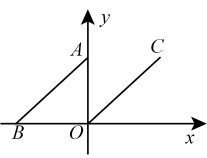2. 把 $y = 3 x$ 的图像向上平移3个单位，则下列各点中，在平移后的直线上的点是（）

A、 $(0 ， - 3)$ B、 $(0 ， 3)$ C、 $(1 ， 5)$ D、 $(- 1 ， 6)$

查看试题解析
3. 如图，在平面直角坐标系中，点 $A$ 的坐标是 $(1 ， 3)$ ，将线段 $O A$ 向右平移5个单位长度，得到线段 $B C$ ，则点 $A$ 的对应点 $C$ 的坐标为（）

A、 $(6 ， 3)$ B、 $(5 ， 3)$ C、 $(5 ， 5)$ D、 $(6 ， 5)$

查看试题解析
4. 点P（-1，2）是由点Q（0，-1）经过（）而得到的．

A、先向右平移1个长度，再向下平移3个单位长度 B、先向左平移1个长度，再向下平移3个单位长度 C、先向上平移3个长度，再向左平移1个单位长度 D、先向下平移1个长度，再向右平移3个单位长度

查看试题解析
5. 如图，以下四个图标中可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
6. 若把点A(－5m，2m－1)向上平移3个单位后得到的点在x轴上，则点A在(　　)

A、x轴上 B、第三象限 C、y轴上 D、第四象限

查看试题解析
7. 如图， $△ A B C$ 经过平移得到 $△ D E F$ ， DE分别交BC，AC于点G，H，若 $∠ B = 97 °$ ， $∠ C = 40 °$ ，则 $∠ G H C$ 的度数为（　　）

A、147° B、40° C、97° D、43°

查看试题解析
8. 如图，△AOB中，∠AOB=90°，现在将△AOB绕点O逆时针旋转44°，得到△A'OB'，则∠A'OB的度数为（）

A、44° B、66° C、56° D、46°

查看试题解析
9. 如图， $△ A B C$ 绕点 $C$ 顺时针旋转 $70 °$ 到 $△ D E C$ 的位置.如果 $∠ E C D = 30 °$ ，那么 $∠ A C E$ 等于（）

A、 $70 °$ B、 $50 °$ C、 $40 °$ D、 $30 °$

查看试题解析
10. 如图，直角坐标系中， $R t △ A O B$ 的顶点A在x轴上， $∠ B = 90 °$ ， $O A = 5$ ， $O B = 3$ ，现将 $△ A O B$ 绕原点O按顺时针方向旋转，得到 $△ D O C$ ，且点C在x轴上，则点D的坐标是（　　）

A、 $(3 ， 4)$ B、 $(3 ， 5)$ C、 $(5 ， 4)$ D、 $(4 ， 5)$

查看试题解析

二、填空题（每题3分，共18分）

11. 已知点B的坐标为（-5，1），它向右平移4个单位长度，再向上平移2个单位长度，得到点B′，则点B′的坐标为．

查看试题解析
12. 如图， $△ A B C$ 以点C为旋转中心，旋转后得到 $△ E D C$ ，已知 $A B = 1.5 ， B C = 4 ， A C = 5$ ，则 $D E =$ ．

查看试题解析
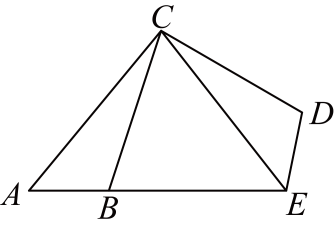13. 如图， $△ A^{'} B^{'} C^{'}$ 是由△ABC沿射线AC方向平移2cm得到的，若 $A C = 3$ cm，则 $A^{'} C =$ cm．

查看试题解析
14. 如图，将 $△ A O B$ 绕点O按逆时针方向旋转 $50 °$ 后得到 $△ A^{'} O B^{'}$ ，若 $∠ A O B = 15 °$ ，则 $∠ A O B^{^{'}}$ 的度数是．

查看试题解析
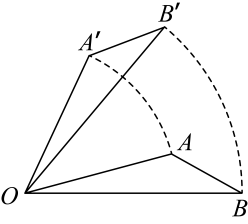15. 如图，△ABC绕点A按逆时针方向旋转50°后的图形为△AB₁C₁ ，则∠ABB₁＝ .

查看试题解析
16. 如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是．

查看试题解析

三、解答题（共7题，共72分）

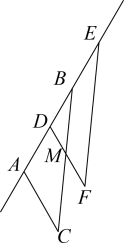
17. 如图，将 $△ A B C$ 沿着直线AB平移得到 $△ D E F$ ， BC与DF相交于点M ，若 $∠ B A C = 100 °$ ， $∠ D E F = 30 °$ ，请求∠FMC的度数．

查看试题解析
18.
如图，Rt△ABC中，∠C = 90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上．

（1）若∠BDA = 70°，求∠BAC的度数．
（2）若BC = 8，AC = 6，求△ABD中AD边上的高．

查看试题解析
19. 如图，在平面直角坐标系中， $Rt △ A B C$ 的三个顶点分别是 $A (- 4 ， 1) ， B (- 1 ， 3) ， C (- 1 ， 1)$ ．

(1)、 $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 关于点O成中心对称，画出对应的 $△ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A B C$ 以点 $(0 ， - 1)$ 为旋转中心顺时针旋转 $90 °$ ，画出旋转后对应的 $△ A_{2} B_{2} C_{2}$ ；

(3)、若将 $△ A_{2} B_{2} C_{2}$ 看作由 $△ A_{1} B_{1} C_{1}$ 旋转得到的，那么旋转角的度数为，旋转中心坐标为．

查看试题解析
20. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．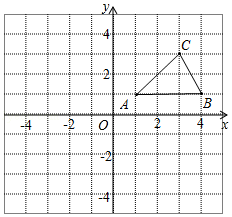

(1)、将△ABC向下平移5个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、将△ABC绕原点O逆时针旋转90°后得到△A₂B₂C₂ ，请画出△A₂B₂C₂；

(3)、判断以O，A₁ ， B为顶点的三角形的形状．（无须说明理由）

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm．

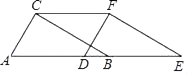(1)、求△ABC向右平移的距离AD的长；

(2)、求四边形AEFC的面积．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A C ， B D$ 是对角线， $△ A B C$ 是等边三角形，将线段 $C D$ 绕点C顺时针旋转 $60 °$ 得到线段 $C E$ ，连接 $A E ， D E$ ．

(1)、求证： $∠ B C D = ∠ A C E$ ；

(2)、若 $∠ A D C = 30 ° ， A D = 6 ， B D = 10$ ，求 $D E$ 的长．

查看试题解析
23. 如图的平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（4，3），B（3，1），C（1，2）．

(1)、将三角形ABC三个顶点的横坐标都减去6，分别得到A₁、B₁、C₁ ，依次连接A₁ ， B₁ ， C₁ ，各点，请写出A₁、B₁、C₁的坐标并画出△A₁B₁C₁ ，并判断所得三角形A₁B₁C₁与三角形ABC的大小、形状和位置有什么关系？

(2)、将三角形ABC三个顶点的纵坐标都减去5，分别得到A₂、B₂、C₂ ，依次连接A₂ ， B₂ ， C₂ ，各点，请写出A₂、B₂、C₂的坐标并画出△A₂B₂C₂ ，并判断所得三角形A₂B₂C₂与三角形ABC的大小、形状和位置有什么关系？

(3)、求△A₂B₂C₂的面积．

查看试题解析