北师大版数学八年级下册单元清测试(第二章)基础卷
试卷更新日期:2024-02-21 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 不等式的解集是( )A、 B、 C、 D、2. 若m>n,则下列不等式正确的是( )A、m﹣2<n﹣2 B、 C、6m<6n D、﹣8m>﹣8n3. 不等式组的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 小霞原有存款52元,小明原有存款70元从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为( )A、52+15n>70+12n B、52+15n<70+12n C、52+12n>70+15n D、52+12n<70+15n5. 若不等式组有解,则a的取值范围是( )A、a>-1 B、a≥-1 C、a≤1 D、a<16. 若不等式(a-2)x>4的解集为 ,则a的取值范围是( )A、a<2 B、a>2 C、a≥2 D、a≤27. 如图,是不等式组的解集在数轴上的正确表示,则的值是( )
4. 小霞原有存款52元,小明原有存款70元从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为( )A、52+15n>70+12n B、52+15n<70+12n C、52+12n>70+15n D、52+12n<70+15n5. 若不等式组有解,则a的取值范围是( )A、a>-1 B、a≥-1 C、a≤1 D、a<16. 若不等式(a-2)x>4的解集为 ,则a的取值范围是( )A、a<2 B、a>2 C、a≥2 D、a≤27. 如图,是不等式组的解集在数轴上的正确表示,则的值是( )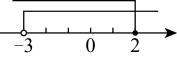 A、 B、 C、6 D、98. 已知,一次函数和的图像交于点 , 且直线交轴于点 . 则的解集( ).
A、 B、 C、6 D、98. 已知,一次函数和的图像交于点 , 且直线交轴于点 . 则的解集( ). A、 B、 C、 D、9. 若不等式组无解,则的取值范围是( )A、 B、 C、 D、10. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、9. 若不等式组无解,则的取值范围是( )A、 B、 C、 D、10. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 关于x的一次函数 , 若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是.12. 如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程是关于x的不等式组的关联方程,则n的取值范围是 .13. 如图,数轴上所表示的x的取值范围为 .
 14. 不等式组 的最小整数解是.15. 若 为有理数,且 的值大于1,则 的取值范围为 .16. 在平面直角坐标系xOy中,一次函数和的图象如图所示.则关于x的一元一次不等式的解集是 .
14. 不等式组 的最小整数解是.15. 若 为有理数,且 的值大于1,则 的取值范围为 .16. 在平面直角坐标系xOy中,一次函数和的图象如图所示.则关于x的一元一次不等式的解集是 .
三、解答题(共9题,共72分)
-
17. 解不等式组 ,并写出满足不等式组的所有整数解.18. 解不等式组 ,并把解集在数轴上表示出来.
 19. 解下列不等式组 , 并把它的解集表示在数轴上.20. 已知不等式5x-2<6x+1.(1)、解该不等式.(2)、若该不等式的最小整数解是方程=6的解,求a的值.21. 对于任意实数 , ,定义关于“ ”的一种运算如下: .例如: ,(1)、若 ,求 的值;(2)、若 ,求 的取值范围.22. 如图,已知直线 ,直线 相交于点A,直线 与x轴交于点 .
19. 解下列不等式组 , 并把它的解集表示在数轴上.20. 已知不等式5x-2<6x+1.(1)、解该不等式.(2)、若该不等式的最小整数解是方程=6的解,求a的值.21. 对于任意实数 , ,定义关于“ ”的一种运算如下: .例如: ,(1)、若 ,求 的值;(2)、若 ,求 的取值范围.22. 如图,已知直线 ,直线 相交于点A,直线 与x轴交于点 . (1)、求直线 的解析式和点A的坐标;(2)、直接写出关于x的不等式 的解集.23. 某学校准备印刷一批证书,现有两个印刷厂可供选择: 甲厂收费方式:收制版费1000元,每本印刷费0.5元;乙厂收费方式:不收制版费,每本收印刷费1.5元;若该校印制证书x本.(1)、当印制证书3000本时,甲厂的收费为元,乙厂的收费为元;(2)、请问印刷多少本证书时,甲乙两厂收费相同?(3)、你认为选择哪一家印刷厂更优惠?24. 4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心.某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)、求直线 的解析式和点A的坐标;(2)、直接写出关于x的不等式 的解集.23. 某学校准备印刷一批证书,现有两个印刷厂可供选择: 甲厂收费方式:收制版费1000元,每本印刷费0.5元;乙厂收费方式:不收制版费,每本收印刷费1.5元;若该校印制证书x本.(1)、当印制证书3000本时,甲厂的收费为元,乙厂的收费为元;(2)、请问印刷多少本证书时,甲乙两厂收费相同?(3)、你认为选择哪一家印刷厂更优惠?24. 4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心.某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:车 型
运往地
甲 地(元/辆)
乙 地(元/辆)
大货车
720
800
小货车
500
650
(1)、求这两种货车各用多少辆?(2)、如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);(3)、在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.25. 如图,已知函数y1=x+5的图象与x轴交于点A,一次函数y2=-2x+b的图象分别与x轴、y轴交于点B,C,且与y1=x+5的图象交于点D(m,4). (1)、求m,b的值;(2)、若y1>y2 , 则x的取值范围是 ;(3)、求四边形AOCD的面积.
(1)、求m,b的值;(2)、若y1>y2 , 则x的取值范围是 ;(3)、求四边形AOCD的面积.