2024年北师大版数学八年级下册周测卷（第二章第5-6节）培优卷

试卷更新日期：2024-02-21 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如果不等式组 ${\begin{array}{l} x + 5 < 4 x - 1 \\ x > m \end{array}$ 的解为 $x > 2$ ，那么 $m$ 的取值范围是（）

A、 $m ⩽ 2$ B、 $m ⩾ 2$ C、 $m > 2$ D、 $m < 2$

查看试题解析
2. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象与 $y = - 2 x$ 的图象交于点 $(m ， - 4)$ ．则对于不等式 $\underset{˙}{k} \underset{˙}{x} \underset{˙}{-} \underset{˙}{b} < - 2 x$ ，下列说法正确的是（）

A、当 $k < - 2$ 时， $x > 2$ B、当 $k < - 2$ 时， $x < 2$ C、当 $k > - 2$ 且 $k \neq 0$ 时， $x > - 2$ D、当 $k > - 2$ 且 $k \neq 0$ 时， $x < - 2$

查看试题解析
3. 函数 $y = | x + 1 | - 2$ ，当 $m \leq x \leq 4$ ，对应 $y$ 的取值范围为 $- 2 \leq y \leq 3$ ，则 $m$ 的取值范围为（）

A、 $m = - 1$ B、 $m \leq - 1$ C、 $- 1 \leq m < 4$ D、 $- 6 \leq m \leq - 1$

查看试题解析
4. 如图，直线y＝kx+b交x轴于点A（﹣2，0），直线y＝mx+n交x轴于点B（5，0），这两条直线相交于点C（2，c），则关于x的不等式组 $\{\begin{matrix} k x + b ＜ 0 \\ m x + n ＞ 0 \end{matrix}$ 的解集为（）

A、x＜5 B、1＜x＜5 C、﹣2＜x＜5 D、x＜﹣2

查看试题解析
5. 已知关于x的不等式组 ${\begin{array}{l} x + 1 \geq 2 \\ x - m < 0 \end{array}$ 有整数解，则 $m$ 的取值范围是（）

A、 $m \geq 2$ B、 $m \leq 2$ C、 $m > 1$ D、 $m \geq 1$

查看试题解析
6. 如图，一次函数y₁=ax+b（a，b是常数）的图象与y轴、x轴分别交于点A（0，3）、点B，正比例函数y₂= $\frac{1}{3}$ x的图象与一次函数y₁的图象交于点P（m，1），有下列结论：
①一次函数y₁的图象与y轴交点的纵坐标为3；
②方程ax+b=0的解为x=4.5；
③不等式ax+b<0的解集为x>4.5，其中正确的有（）

A、3个 B、2个 C、1个 D、0个

查看试题解析
7. 已知关于x的不等式组 ${\begin{cases} x - a \geq 0 \\ 3 - 2 x > 0 \end{cases}$ 的整数解共有4个，则a的取值范围是（）

A、﹣3＜a≤﹣2 B、﹣3≤a＜﹣2 C、﹣3＜a＜﹣2 D、a＜﹣2

查看试题解析
8. 小明去商店购买A、B两种玩具，共用了10元钱，A种玩具每件1元，B种玩具每件2元.若每种玩具至少买一件，且A种玩具的数量多于B种玩具的数量.则小明的购买方案有（）

A、5种 B、4种 C、3种 D、2种

查看试题解析
9. 已知不等式组 ${\begin{cases} x - a > 2 \\ x + 1 < b \end{cases}$ 的解集是 $- 1 ＜ x ＜ 1$ ，则 $(a + b)^{2023}$ =（）

A、0 B、-1 C、1 D、2023

查看试题解析
10. 若不等式组 ${\begin{array}{l} x - 2 < 3 x - 6 ， \\ x < m \end{array}$ 无解，则 $m$ 的取值范围是（）

A、 $m > 2$ B、 $m < 2$ C、m≥2 D、m≤2

查看试题解析

二、填空题（每题3分，共18分）

11. 若关于 $x$ 的不等式组 ${\begin{array}{l} 2 x + 1 > x + a ， \\ \frac{x}{2} + 1 ⩾ \frac{5}{2} x - 9 \end{array}$ 的所存整数解的和为14，则整数 $a$ 的值为.

查看试题解析
12. 已知关于x ， y的方程组 ${\begin{array}{l} 2 x + 3 y = 5 \\ 3 x + 2 y = a \end{array}$ 的解满足 $y - x > 0$ ，且关于x的不等式组 ${\begin{array}{l} \frac{x + 3}{2} - 2 > a \\ x + 1 < a \end{array}$ 无解，那么所有符合条件的整数a的和为．

查看试题解析
13. 如图，已知函数y＝﹣x+b与函数y＝kx+7的图象交于点P（﹣2，3），则关于x的不等式﹣x+b≤kx+7的解集是．

查看试题解析
14. 如图，一次函数y₁＝kx+b与y₂＝mx+n的图象相交于点（1，3），则方程组 ${\begin{cases} y_{1} = k x + b \\ y_{2} = m x + n \end{cases}$ 的解为 ${\begin{cases} x = 1 \\ y = 3 \end{cases}$ ，关于x的不等式kx+b＞mx+n的解为．

查看试题解析
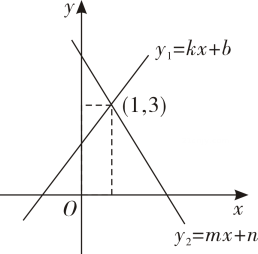15.
如图：函数y=2x和y=ax+4的图象交于点A（m，2），不等式2x＜ax+4的解集为．

查看试题解析
16. 如图，在平面直角坐标系中，函数 $y = 2 x$ 与 $y = k x + b (k < 0)$ 的图象交于点 $P (m ， 2)$ ，则不等式 $k x + b > 2 x$ 的解集为．

查看试题解析

三、解答题（共9题，共72分）

17. 解不等式组 ${\begin{array}{l} 4 x - 3 (x - 2) \geq 4 ① \\ \frac{x - 1}{5} > \frac{x + 1}{2} - 1 ② \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
18. 解不等式组 ${\begin{array}{l} x < \frac{x + 3}{2} ， ① \\ 2 (x + 2) \geq x + 1 ， ② \end{array}$ 并把解集在数轴上表示出来.

查看试题解析
19. 解不等式组： ${\begin{array}{l} x - 2 \leq 3 (x + 1) \\ x - \frac{3}{2} > \frac{4 x - 5}{3} \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
20. 已知关于x，y的方程满足方程组 ${\begin{cases} 3 x + 2 y = m + 1 \\ 2 x + y = m - 1 \end{cases}$ ．

(1)、若x-y＝2，求m的值；

(2)、若x，y，m均为非负数，求m的取值范围，并化简式子|m-3|+|m-5|；

查看试题解析
21. 已知方程 $2 x - 3 = 1$ 与不等式 $x + 3 > 0$ ，当 $x = 2$ 时， $2 x - 3 = 2 \times 2 - 3 = 1$ ， $x + 3 = 2 + 3 = 5 > 0$ 同时成立，则称“ $x = 2$ ”是方程 $2 x - 3 = 1$ 与不等式 $x + 3 > 0$ 的“完美解”．

(1)、已知 $① 2 x + 1 > 3$ ， $② 3 x + 7 < 4$ ， $③ 2 - x > 2 x + 1$ ，则方程 $2 x + 3 = 1$ 的解是不等式 $($ 填序号 $)$ 的“完美解”；

(2)、若 ${\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 是方程组 ${\begin{array}{l} x + 2 y = a \\ 2 x + y = 2 a + 3 \end{array}$ 与不等式 $x + y > 3$ 的一组“完美解”，求 $a$ 的取值范围；

(3)、若 ${\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 是方程 $x - 3 y = 5$ 与不等式组 ${\begin{array}{l} x > 2 \\ y < 1 \end{array}$ 的“完美解”，求 $x_{0} + 3 y_{0}$ 的取值范围．

查看试题解析
22. “一盔一带”安全守护行动是公安部在全国开展的一项安全守护行动，也是营造文明城市，做文明市民的重要标准，“一盔”是指安全头盔，电动自行车驾驶人和乘坐人员应当戴安全头盔，某商场欲购进一批头盔，已知购进8个甲型头盔和6个乙型头盔需要630元，购进6个甲型头盔和8个乙型头盔需要700元．

(1)、购进1个甲型头盔和1个乙型头盔分别需要多少元？

(2)、若该商场准备购进200个这两种型号的头盔，总费用不超过10200元，以甲型头盔58元/个、乙型头盔98元/个的价格销售完．要使总利润不少于6180元，有多少种进货方案？其中利润最大的方案是甲型头盔和乙型头盔各多少个？最大利润是多少？

查看试题解析
23. 我市某化工厂现有甲种原料290kg，乙种原料212kg，计划利用这两种原料生产A，B两种产品共80件．生产一件A产品需要甲种原料5kg，乙种原料1.5kg，生产成本是120元；生产一件B产品，需要甲种原料2.5kg，乙种原料3.5kg，生产成本是200元．

(1)、该化工厂现有的原料能否保证生产？若能的话，有几种生产方案，请你设计出来；

(2)、设生产A，B两种产品的总成本为y元，设A种的生产件数为x，试写出y与x之间的函数关系，并利用函数的性质说明（1）中哪种生产方案总成本最低？最低生产总成本是多少？

查看试题解析
24. 如图，已知函数 $y_{1} = 3 x + b$ 和 $y_{2} = a x - 2$ 的图象交于点 $P (- 1 ， - 4)$ ，这两个函数的图象与 $x$ 轴分别交于点 $A$ 、 $B$ ．

(1)、分别求出这两个函数的解析式；

(2)、求 $△ A B P$ 的面积；

(3)、根据图象直接写出不等式 $3 x + b + 2 \leq a x$ 的解集．

查看试题解析
25. 对非负数x“四舍五入”到个位的值记为〈x〉，即当n为非负整数时，若n﹣0.5≤x＜n+0.5，则〈x〉＝n.反之，当n为非负整数时，若〈x〉＝n，则n﹣0.5≤x＜n+0.5.如〈1.34〉＝1，〈4.86〉＝5.

(1)、〈π〉＝；

(2)、若〈0.5x﹣1〉＝7，则实数x的取值范围是；

(3)、若关于x的不等式组 ${\begin{matrix} \frac{2 x - 1}{3} \geq - 1 \\ x - 〈 a 〉 < 0 \end{matrix}$ 的整数解恰有4个，求a的取值范围；

(4)、满足〈x〉＝ $\frac{6}{5}$ x的所有非负数x的值为 .

查看试题解析