2024年北师大版数学八年级下册周测卷(第二章第5-6节)基础卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,直线过点 , , 则不等式的解集是( )
 A、 B、 C、 D、2. 不等式组的解在数轴上表示正确的是( )A、
A、 B、 C、 D、2. 不等式组的解在数轴上表示正确的是( )A、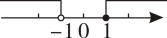 B、
B、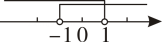 C、
C、 D、
D、 3. 若函数的图象如图所示,则关于的不等式的解集为( )
3. 若函数的图象如图所示,则关于的不等式的解集为( ) A、 B、 C、 D、4. 如图,直线与直线相交于点 , 直线过点 , 则关于的不等式的解集为( )
A、 B、 C、 D、4. 如图,直线与直线相交于点 , 直线过点 , 则关于的不等式的解集为( ) A、 B、 C、 D、5. 不等式组的解集在数轴上表示为( )A、
A、 B、 C、 D、5. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( )
6. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( ) A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为7. 下列不等式组中无解的是( )A、 B、 C、 D、8. 若点(m-1,2m+1)在第二象限,则m的取值范围为( )A、m>1 B、m<- C、-<m<1 D、m>1或m<-9. 若不等式组无解,则的取值范围为( )A、 B、 C、 D、10. 若关于x的不等式组的整数解共有三个,则a的取值范围是( ).A、 B、 C、 D、
A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为7. 下列不等式组中无解的是( )A、 B、 C、 D、8. 若点(m-1,2m+1)在第二象限,则m的取值范围为( )A、m>1 B、m<- C、-<m<1 D、m>1或m<-9. 若不等式组无解,则的取值范围为( )A、 B、 C、 D、10. 若关于x的不等式组的整数解共有三个,则a的取值范围是( ).A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 不等式组的解集是 .12. 某班数学兴趣小组对不等式组 , 进行讨论,得到以下结论:
①若a=5,则不等式组的解为3<x≤5;
②若a=2,则不等式组无解;
③若不等式组无解,则a的取值范围为a<3;
④若不等式组只有两个整数解,则a的值可以为5.
其中,正确结论的序号是.
13. 若关于的一元一次不等式组恰有个整数解,则实数的取值范围是 .14. 如果一元一次不等式组的解集为 , 则的取值范围是 .15. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(2,5),不等式3x-1≥kx解集是 .16. 如图,直线与直线的交点是 , 则不等式的解集是 .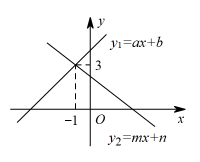
三、解答题(共9题,共72分)
-
17. 解不等式组.(1)、(2)、18. 解不等式组: ,并把它的解集在数轴上表示出来.19. 解不等式组 , 并将不等式组的解集在数轴上表示出来.20. 解不等式组并把解集表示在数轴上: .21. 解下列不等式组 , 并把它的解集表示在数轴上.22. 为改善生态环境,美化居住环境,我市园林管理部门计划在沂河两岸种植水杉树.现甲、乙两家林场有相同的水杉树苗可供选择,具体销售方案如下:
甲林场
乙林场
购树苗数量
销售单价
购树苗数量
销售单价
不超过1000棵
4元
不超过2000棵
4元
超过1000棵的部分
3.8元
超过2000棵的部分
3.6元
设购买水杉树苗 棵,到两家林场购买所需费用分别为 元, 元.
(1)、该村需要购买1500棵水杉树苗,若都在甲林场购买,所需费用为元,若都在乙林场购买所需费用为元;(2)、当 时,分别求出 , 与 之间的函数关系式;(3)、如果你是我市园林管理部门的负责人,选择到哪家林场购买树苗合算?为什么?23. 2017年党中央、国务院设立了雄安新区,它有着丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)、若租用水面 亩,则年租金共需元;(2)、水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);(3)、李大爷现在资金25000元,他准备再向银行贷不超过25000元的款,用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35000元?

