2024年北师大版数学八年级下册周测卷(第二章第1-4节)培优卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图是某桥洞的限高标志,则能通过此桥洞的车辆高度是( )
 A、6.5m B、6m C、5.5m D、4.5m2. 如果 , 那么下列运算正确的是( )A、 B、 C、 D、3. 已知数轴上的点分别表示数 , 其中 , . 若 , 数在数轴上用点表示,则点在数轴上的位置可能是( )A、
A、6.5m B、6m C、5.5m D、4.5m2. 如果 , 那么下列运算正确的是( )A、 B、 C、 D、3. 已知数轴上的点分别表示数 , 其中 , . 若 , 数在数轴上用点表示,则点在数轴上的位置可能是( )A、 B、
B、 C、
C、 D、
D、 4. 若不等式 的解集中 的每一个值,都能使关于 的不等式 成立,则 的取值范围是( )A、 B、 C、 D、5. 已知 , 则下列结论正确的是( )A、 B、 C、 D、6. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣17. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x支签字笔,则下列不等关系正确的是( )A、5×2+2x≥30 B、5×2+2x≤30 C、2×2+2x≥30 D、2×2+5x≤308. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、9. 不等式1-x≥2的解在数轴上表示正确的是( )A、
4. 若不等式 的解集中 的每一个值,都能使关于 的不等式 成立,则 的取值范围是( )A、 B、 C、 D、5. 已知 , 则下列结论正确的是( )A、 B、 C、 D、6. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣17. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x支签字笔,则下列不等关系正确的是( )A、5×2+2x≥30 B、5×2+2x≤30 C、2×2+2x≥30 D、2×2+5x≤308. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、9. 不等式1-x≥2的解在数轴上表示正确的是( )A、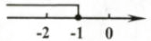 B、
B、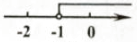 C、
C、 D、
D、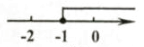 10. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、7
10. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、7二、填空题(每题3分,共18分)
-
11. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.12. 若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取值范围是 .13. 对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=ll.请根据上述的定义解决问题:若不等式3※x<2,则不等式的正整数解是 .
14. 若不等式(a﹣3)x>1的解集为x< ,则a的取值范围是 .15. 已知不等式的解集为 , 则a的值为.16. 世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有人进公园,买40张门反而合算.三、解答题(共9题,共72分)
-
17. 解不等式: .18. 求不等式的正整数解.19. 解不等式: , 并写出它的正整数解.20. 当x取何正整数时,代数式的值不小于代数式的值?21. 如图,在数轴上,点分别表示数 , , 且点在点的左侧.(1)、求的取值范围;(2)、若点表示的数是关于的不等式的解,求的整数解.
 22. 已知方程组 的解满足 ,求k的取值范围.23. 某古镇为发展旅游产业,吸引更多的游客前往游览,助力乡村振兴,决定在“五一”期间对团队*旅游实行门票特价优惠活动,价格如下表:
22. 已知方程组 的解满足 ,求k的取值范围.23. 某古镇为发展旅游产业,吸引更多的游客前往游览,助力乡村振兴,决定在“五一”期间对团队*旅游实行门票特价优惠活动,价格如下表:购票人数(人)
每人门票价(元)
60
50
40
*题中的团队人数均不少于10人
现有甲、乙两个团队共102人,计划利用“五一”假期到该古镇旅游,其中甲团队不足50人,乙团队多于50人.
(1)、如果两个团队分别购票,一共应付5580元,问甲、乙团队各有多少人?(2)、如果两个团队联合起来作为一个“大团队”购票,比两个团队各自购票节省的费用不少于1200元,问甲团队最少多少人?24. 为落实“五育并举”,绿化美化环境,学校在劳动周组织学生到校园周边种植甲、乙两种树苗.已知购买甲种树苗3棵,乙种树苗2棵共需12元;购买甲种树苗1棵,乙种树苗3棵共需11元.(1)、求每棵甲、乙树苗的价格.(2)、本次活动共种植了200棵甲、乙树苗,假设所种的树苗若干年后全部长成了参天大树,并且平均每棵树的价值(含生态价值,经济价值)均为原来树苗价的100倍,要想获得不低于5万元的价值,请问乙种树苗种植数量不得少于多少棵?25. 学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师现有甲、乙两种大型客车,它们的载客量和租金如表所示:甲型客车
乙型客车
载客量人辆
租金元辆
(1)、参加本次实践活动的老师和学生各有多少名?(2)、租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车辆;(3)、学校共有几种租车方案?最少租车费用是多少?