北师大版数学八年级下册单元清测试(第一章)培优卷
试卷更新日期:2024-02-21 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是( )
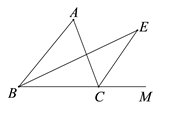 A、15° B、30° C、45° D、60°2. 已知实数x,y满足 ,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对3. 如图,在中, , 以点为圆心,适当长为半径作弧,分别交于点 , 分别以点为圆心,大于的长为半径作弧,两弧在的内部相交于点 , 作射线 , 交于点 , 则的长为( )
A、15° B、30° C、45° D、60°2. 已知实数x,y满足 ,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对3. 如图,在中, , 以点为圆心,适当长为半径作弧,分别交于点 , 分别以点为圆心,大于的长为半径作弧,两弧在的内部相交于点 , 作射线 , 交于点 , 则的长为( ) A、 B、 C、 D、4. 如图,在四边形中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交于E,F两点;②分别以点E,F为圆心以大于的长为半径画弧,两弧交于点P;③连接并延长交于点G.则的长是( )
A、 B、 C、 D、4. 如图,在四边形中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交于E,F两点;②分别以点E,F为圆心以大于的长为半径画弧,两弧交于点P;③连接并延长交于点G.则的长是( ) A、2 B、3 C、4 D、55. 如图,点 D在 △ABC的边BC上,点 P在射线 AD上(不与点 A,D重合),连接PB, PC.下列命题中,假命题是( )
A、2 B、3 C、4 D、55. 如图,点 D在 △ABC的边BC上,点 P在射线 AD上(不与点 A,D重合),连接PB, PC.下列命题中,假命题是( )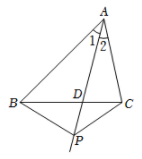 A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则6. 如图,在中,与的平分线交于点 , 过点作 , 分别交、于点、若 , , 则的周长为( )
A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则6. 如图,在中,与的平分线交于点 , 过点作 , 分别交、于点、若 , , 则的周长为( )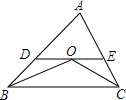 A、 B、 C、 D、7. 如图,是的角平分线, , 垂足为 , 交的延长线于点 , 若恰好平分 , .给出下列四个结论:①;②;③;④ , 其中正确的结论共有( )
A、 B、 C、 D、7. 如图,是的角平分线, , 垂足为 , 交的延长线于点 , 若恰好平分 , .给出下列四个结论:①;②;③;④ , 其中正确的结论共有( ) A、4个 B、3个 C、2个 D、1个8. 如图,点P是内部的一点,点P到三边AB、AC、BC的距离 . 若 , 则 ( )
A、4个 B、3个 C、2个 D、1个8. 如图,点P是内部的一点,点P到三边AB、AC、BC的距离 . 若 , 则 ( ) A、 B、 C、 D、9. 如图,“三等分角器”是由两根有槽的棒 , 组成,两根棒在点相连,并可绕点转动,点固定, , 可在槽内滑动, , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图,“三等分角器”是由两根有槽的棒 , 组成,两根棒在点相连,并可绕点转动,点固定, , 可在槽内滑动, , 若 , 则的度数为( ) A、 B、 C、 D、10. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作正三角形ABC和正三角形CDE , 连接AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ.以下四个结论:①;②;③;④.其中正确的结论个数是( )
A、 B、 C、 D、10. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作正三角形ABC和正三角形CDE , 连接AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ.以下四个结论:①;②;③;④.其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 将含角的直角三角板和直尺按如图所示的方式放置,已 , 点 , 表示的刻度分别为 , 则线段的长为cm.
 12. 如图,AE=AB , ∠E=∠B,EF=BC , 若∠EAB=52°,则∠EFA= .
12. 如图,AE=AB , ∠E=∠B,EF=BC , 若∠EAB=52°,则∠EFA= . 13. 已知一张三角形纸片如图甲 , 其中 , 将纸片沿过点的直线折叠,使点落到边上的点处,折痕为如图乙 , 再将纸片沿过点的直线折叠,点恰好与点重合,折痕为如图丙原三角形纸片中,的大小为 .
13. 已知一张三角形纸片如图甲 , 其中 , 将纸片沿过点的直线折叠,使点落到边上的点处,折痕为如图乙 , 再将纸片沿过点的直线折叠,点恰好与点重合,折痕为如图丙原三角形纸片中,的大小为 .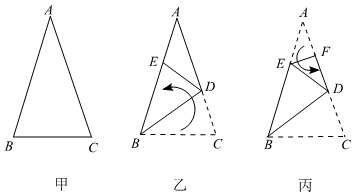 14. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是°.
14. 如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是°. 15. 如图,在直角坐标系中,长方形的顶点分别在轴,轴上,点的坐标分别为为边上一点,点的坐标为 , 若是腰长为5的等腰三角形,则点的坐标是 .
15. 如图,在直角坐标系中,长方形的顶点分别在轴,轴上,点的坐标分别为为边上一点,点的坐标为 , 若是腰长为5的等腰三角形,则点的坐标是 . 16. 已知,都是边长为2的等边三角形,按下图所示摆放.点都在x轴正半轴上,且 , 则点的坐标是 .
16. 已知,都是边长为2的等边三角形,按下图所示摆放.点都在x轴正半轴上,且 , 则点的坐标是 .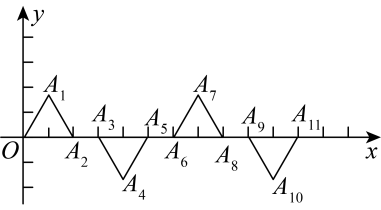
三、解答题(共8题,共72分)
-
17. 如图, , 为上一点, , 并且
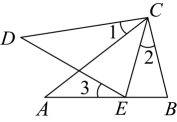 (1)、求证:;(2)、若 , 则= .18. 如图,中, , 点分别在边上, , .
(1)、求证:;(2)、若 , 则= .18. 如图,中, , 点分别在边上, , .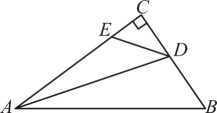 (1)、求证:平分;(2)、写出与的数量关系,并说明理由.19. 如图,的延长线于 , 于 , 若 , .
(1)、求证:平分;(2)、写出与的数量关系,并说明理由.19. 如图,的延长线于 , 于 , 若 , . (1)、求证:;(2)、求证:平分.20. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
(1)、求证:;(2)、求证:平分.20. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.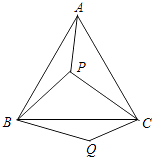 (1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.21. 如图,在中, , 将绕点逆时针旋转至处,分别延长与交于点 , 连接、 .
(1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.21. 如图,在中, , 将绕点逆时针旋转至处,分别延长与交于点 , 连接、 . (1)、求证:平分;(2)、若 , , 求的长.22. 如图①,中, , 、的平分线交于点,过点作EFBC交、于、 .
(1)、求证:平分;(2)、若 , , 求的长.22. 如图①,中, , 、的平分线交于点,过点作EFBC交、于、 . (1)、图①中有几个等腰三角形?猜想:与、之间有怎样的关系.(2)、如图②,若 , 其他条件不变,在第(1)问中与、间的关系还存在吗?(3)、如图③,若中的平分线与平分线交于 , 过点作OEBC,交于 , 交于 . 与、关系又如何?说明你的理由.23. 教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.
(1)、图①中有几个等腰三角形?猜想:与、之间有怎样的关系.(2)、如图②,若 , 其他条件不变,在第(1)问中与、间的关系还存在吗?(3)、如图③,若中的平分线与平分线交于 , 过点作OEBC,交于 , 交于 . 与、关系又如何?说明你的理由.23. 教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.2.线段垂直平分线
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连接PA、PB , 将线段AB沿直线MN对折,我们发现PA与PB完全重合,由此即有:线段垂直平分线的性质定理线段垂直平分线上的点到线段两端钓距离相等。
已知:如图, , 垂足点为C , , 点P是直线MN的任意一点。
求证:。
分析:图中有两个直角三角形APC和BPC , 只要证明这两个三角形全等,便可证明。
请写出完整的证明过程

 (1)、定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.(2)、定理应用:
(1)、定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,在中,直线m、n分别是边BC、AC的垂直平分线,直线m、n交于点O , 过点O作于点H . 求证: .
(3)、如图③,在中, , 边AB的垂直平分线交AC于点D , 边BC的垂直平分线交AC于点E . 若 , , 则DE的长为 .24. 在中, . (1)、如图①,如果 , 是中边上的高,并且 , 则°;(2)、如图②,如果 , 是中边上的高,并且 , 则°;(3)、由(1),(2)猜想:与之间有什么数量关系?请用式子表示:;(4)、如图③,如果不是中BC边上的高,但仍有 , 请判断与之间是否仍然存在(3)中的数量关系?请说明理由.
(1)、如图①,如果 , 是中边上的高,并且 , 则°;(2)、如图②,如果 , 是中边上的高,并且 , 则°;(3)、由(1),(2)猜想:与之间有什么数量关系?请用式子表示:;(4)、如图③,如果不是中BC边上的高,但仍有 , 请判断与之间是否仍然存在(3)中的数量关系?请说明理由.