北师大版数学八年级下册单元清测试(第一章)基础卷
试卷更新日期:2024-02-21 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
 A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点2. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°3. 如图.在△ABC中,AB=AC.D是BC上一点,DE⊥AB于点E,若∠A=50",则∠BDE的度数是( )
A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点2. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°3. 如图.在△ABC中,AB=AC.D是BC上一点,DE⊥AB于点E,若∠A=50",则∠BDE的度数是( ) A、65° B、50° C、30° D、25°4. 如图,在中,过点B作的角平分线的垂线,垂足为F,交于点G,若 , 则线段的长为( )
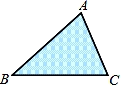
A、65° B、50° C、30° D、25°4. 如图,在中,过点B作的角平分线的垂线,垂足为F,交于点G,若 , 则线段的长为( ) A、1 B、2 C、2.5 D、35. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论中,不正确的是( )
A、1 B、2 C、2.5 D、35. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.下列结论中,不正确的是( )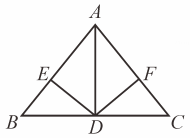 A、DA平分∠EDF B、AE=AF C、AD上任一点P到AB,AC的距离相等 D、AB,AC上的点到AD的距离相等6. 等腰三角形的一边长为 , 另一边长为 , 则该等腰三角形的周长为( )A、 B、 C、或 D、或7. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论不一定正确的是( )
A、DA平分∠EDF B、AE=AF C、AD上任一点P到AB,AC的距离相等 D、AB,AC上的点到AD的距离相等6. 等腰三角形的一边长为 , 另一边长为 , 则该等腰三角形的周长为( )A、 B、 C、或 D、或7. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论不一定正确的是( ) A、∠B=∠C B、AB=2BD C、AD⊥BC D、BD=CD8. 如图,在中, , , 边的垂直平分线分别交 , 于 , 两点,则的周长为( )
A、∠B=∠C B、AB=2BD C、AD⊥BC D、BD=CD8. 如图,在中, , , 边的垂直平分线分别交 , 于 , 两点,则的周长为( )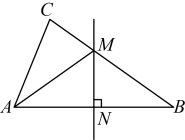 A、 B、 C、 D、9. 如图所示,已知 , 用尺规在线段上确定一点 , 使得 , 则符合要求的作图痕迹是( )A、
A、 B、 C、 D、9. 如图所示,已知 , 用尺规在线段上确定一点 , 使得 , 则符合要求的作图痕迹是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,OD平分于点是射线OB上的任一点,则DF的长度不可能是( )
10. 如图,OD平分于点是射线OB上的任一点,则DF的长度不可能是( )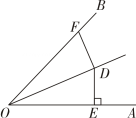 A、2.8 B、3 C、4.2 D、5
A、2.8 B、3 C、4.2 D、5二、填空题(每题3分,共18分)
-
11. 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,已知△BCE的周长是15,AC比BC长3,则AC长为 .
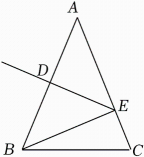 12. 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么点M到线段AB的距离是.
12. 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么点M到线段AB的距离是. 13. 如图所示,添加一个条件可使用“”判定与全等可以添加的条件是 .
13. 如图所示,添加一个条件可使用“”判定与全等可以添加的条件是 .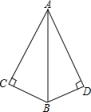 14. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .
14. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .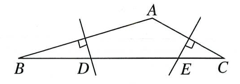 15. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 .
15. 如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 . 16. 如图,平行四边形中,的平分线交于 , , , 则的长为 .
16. 如图,平行四边形中,的平分线交于 , , , 则的长为 .
三、解答题(共8题,共72分)
-
17. 如图,在的正方形网格中,点A , B , C均在格点上,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
 (1)、在图(1)中作的平分线;(2)、在图(2)中作出直线 , 使直线同时满足以下两个条件:
(1)、在图(1)中作的平分线;(2)、在图(2)中作出直线 , 使直线同时满足以下两个条件:①直线过点C;
②点A , 点B到直线的距离相等.
18. 如图,在 中, 是 边上的中线,E是 边上一点,过点 作 交 的延长线于点F. (1)、求证: .(2)、当 , , 时,求 的长.19. 如图,AB∥CD,直线 EF 分别交 AB、CD于 点 E、F,EG 平分∠AEF,
(1)、求证: .(2)、当 , , 时,求 的长.19. 如图,AB∥CD,直线 EF 分别交 AB、CD于 点 E、F,EG 平分∠AEF, (1)、求证:△EGF 是等腰三角形.(2)、若∠1=40°,求∠2 的度数.20. 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD,
(1)、求证:△EGF 是等腰三角形.(2)、若∠1=40°,求∠2 的度数.20. 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD, (1)、求证:AD=BE(2)、求:∠BFD的度数.21. 如图,在中, .
(1)、求证:AD=BE(2)、求:∠BFD的度数.21. 如图,在中, . (1)、求作:的角平分线交于点E . (要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求的度数.22. 已知:如图,点C为线段上一点, , 都是等边三角形,交于点E,交于点F.
(1)、求作:的角平分线交于点E . (要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 求的度数.22. 已知:如图,点C为线段上一点, , 都是等边三角形,交于点E,交于点F. (1)、求证::(2)、求证:为等边三角形.
(1)、求证::(2)、求证:为等边三角形.