2024年北师大版数学八年级下册周测卷(第一章第3-4节)基础卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
1. 如图,在中, , 点E是斜边的中点, , 且 , 则 ( )
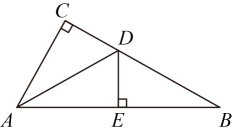 A、60° B、70° C、80° D、90°2. 如图,直线CD是线段AB的垂直平分线,为直线CD上的一点,已知线段 , 则线段PB的长度为( )
A、60° B、70° C、80° D、90°2. 如图,直线CD是线段AB的垂直平分线,为直线CD上的一点,已知线段 , 则线段PB的长度为( ) A、16 B、8 C、6 D、43. 下列选项的尺规作图,能推出的是( )A、
A、16 B、8 C、6 D、43. 下列选项的尺规作图,能推出的是( )A、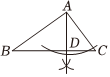 B、
B、
C、 D、
D、 4. 如图,在中,结合尺规作图的痕迹,已知 , 的周长为14cm,则的周长是( )
4. 如图,在中,结合尺规作图的痕迹,已知 , 的周长为14cm,则的周长是( ) A、17cm B、18cm C、19cm D、20cm5. 如图,OD平分∠AOB,DE⊥AO于点E,DE=5,点F是射线OB上的任意一点,则DF的长度不可能是( )
A、17cm B、18cm C、19cm D、20cm5. 如图,OD平分∠AOB,DE⊥AO于点E,DE=5,点F是射线OB上的任意一点,则DF的长度不可能是( )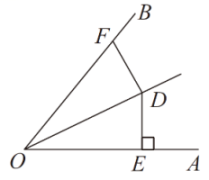 A、4 B、5 C、6 D、76. 如图,在中, , 分别是 , 的平分线.若 , , 则( )
A、4 B、5 C、6 D、76. 如图,在中, , 分别是 , 的平分线.若 , , 则( )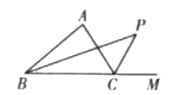 A、70° B、60° C、50° D、40°7. 如图,OC是内部的一条射线,是射线OC上任意一点,.下列条件:①;②;③;④ , 其中,能判定OC是的平分线的有( )
A、70° B、60° C、50° D、40°7. 如图,OC是内部的一条射线,是射线OC上任意一点,.下列条件:①;②;③;④ , 其中,能判定OC是的平分线的有( ) A、1个 B、2个 C、3个 D、4个8. 如图, , 垂足分别为点C,D,则下列结论中错误的是( )
A、1个 B、2个 C、3个 D、4个8. 如图, , 垂足分别为点C,D,则下列结论中错误的是( ) A、 B、 C、 D、9. 为促进旅游发展,某地要在三条公路围成的一块平地上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这个度假村应修建在( )
A、 B、 C、 D、9. 为促进旅游发展,某地要在三条公路围成的一块平地上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这个度假村应修建在( ) A、三条高线的交点处 B、三条中线的交点处 C、三条角平分线的交点处 D、三边垂直平分线的交点处10. 如图, , , 平分 , 则为( )
A、三条高线的交点处 B、三条中线的交点处 C、三条角平分线的交点处 D、三边垂直平分线的交点处10. 如图, , , 平分 , 则为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图:在△ABC中,CE平分∠ACB , CF平分∠ACD , 且EF∥BC交AC于M , 若CM=5,则CE2+CF2= .
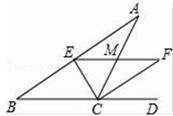 12. 如图,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为 m.
12. 如图,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为 m.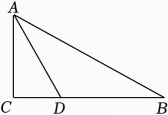 13. 两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P , 其中一把直尺边缘和射线重合,另一把直尺的下边缘与射线重合,连接并延长,若 , 则的度数为 .
13. 两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P , 其中一把直尺边缘和射线重合,另一把直尺的下边缘与射线重合,连接并延长,若 , 则的度数为 . 14. 如图,在中, , 平分交于点 , , , 则 .
14. 如图,在中, , 平分交于点 , , , 则 . 15. 如图,在中,边的垂直平分线交于点 , 交于点 , 若 , , 则的周长是 .
15. 如图,在中,边的垂直平分线交于点 , 交于点 , 若 , , 则的周长是 .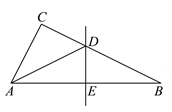 16. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.
16. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.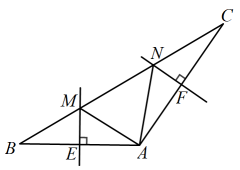
三、解答题
-
17. 如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线DE分别交AB,AC于点D,E.
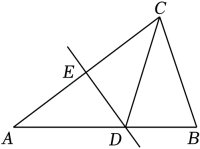 (1)、求证:△BCD是等腰三角形;(2)、若△BCD的周长是13,BC=5,求AC的长.18. 如图,在中,
(1)、求证:△BCD是等腰三角形;(2)、若△BCD的周长是13,BC=5,求AC的长.18. 如图,在中,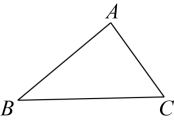 (1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。19. 如图,已知∠A=∠D=90°,点E,F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.
(1)、作的角平分线交于 , 作线段的垂直平分线分别交于 , 交于 , 垂足为(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,连接 , 则与边的位置关系是。19. 如图,已知∠A=∠D=90°,点E,F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.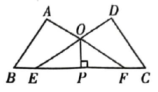 (1)、求证:AF=DE;(2)、若OP⊥EF,求证:OP平分∠EOF.20. 如图,在中,的平分线交于点D,过点D作交于点E.
(1)、求证:AF=DE;(2)、若OP⊥EF,求证:OP平分∠EOF.20. 如图,在中,的平分线交于点D,过点D作交于点E. (1)、求证:;(2)、若 , , 求的度数.21. 人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法;
(1)、求证:;(2)、若 , , 求的度数.21. 人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法;

请你根据提供的材料完成下面问题 .
(1)、这种作已知角的平分线的方法的依据是 . (填序号)① ② ③ ④
(2)、请你证明为的平分线.22. 如图,交延长线于 , 于 , , .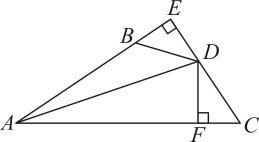 (1)、求证:平分;(2)、直接写出与之间的数量关系.23. 如图,是的角平分线, , 垂足为F,与交于点D.
(1)、求证:平分;(2)、直接写出与之间的数量关系.23. 如图,是的角平分线, , 垂足为F,与交于点D.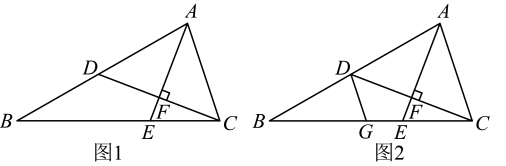 (1)、如图1,若 , , 求的度数;(2)、如图2,点G在线段上,满足 , 求证:与互余.24. 在数学活动课上,老师组织七(1)班的同学开展了探究两角之间数量关系的数学活动.如图,已知射线 , 连接AB,点P是射线AM上一动点(与点A不重合),BC、BD分别平分和 , 分别交射线AM于点C,D.
(1)、如图1,若 , , 求的度数;(2)、如图2,点G在线段上,满足 , 求证:与互余.24. 在数学活动课上,老师组织七(1)班的同学开展了探究两角之间数量关系的数学活动.如图,已知射线 , 连接AB,点P是射线AM上一动点(与点A不重合),BC、BD分别平分和 , 分别交射线AM于点C,D. (1)、【小试牛刀】
(1)、【小试牛刀】当时,求的度数;
(2)、【变式探索】当点P运动时,与之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)、【能力提升】当点P运动到使时,(直接写出结果).