2024年北师大版数学八年级下册周测卷(第一章 第1-2节)培优卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
1. 若等腰三角形有一个内角为 , 则这个等腰三角形的底角是( )A、 B、 C、 D、2. 如图,在中, , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于两点,作直线 , 交边于点 , 连接 , 则的度数为( )
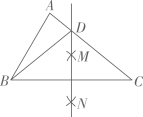 A、 B、 C、 D、3. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于 , 即三个内角都大于 . 则三角形的三个内角的和大于 , 这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于 . 上述推理使用的证明方法是( )A、反证法 B、比较法 C、综合法 D、分析法4. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( )
A、 B、 C、 D、3. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于 , 即三个内角都大于 . 则三角形的三个内角的和大于 , 这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于 . 上述推理使用的证明方法是( )A、反证法 B、比较法 C、综合法 D、分析法4. 如图,是等边的边上的高,以点为圆心,长为半径作弧交的延长线于点 , 则( ) A、 B、 C、 D、5. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
A、 B、 C、 D、5. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ). A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE∥AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE∥AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是( ) A、BF=1 B、DC=3 C、AE=5 D、AC=97. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )
A、BF=1 B、DC=3 C、AE=5 D、AC=97. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )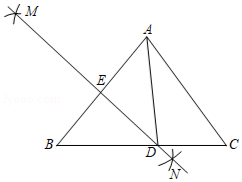 A、30° B、40° C、50° D、60°8. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )
A、30° B、40° C、50° D、60°8. 如图,在中, , 以为圆心,任意长为半径画弧,分别交 , 于点 , , 再分别以 , 为圆心,大于的定长为半径画弧,两弧交于点 , 作射线交于点 , 作 , 垂足为 , 则下列结论不正确的是( )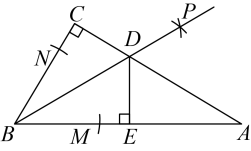 A、 B、 C、 D、一定经过的内心9. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( )
A、 B、 C、 D、一定经过的内心9. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( ) A、4 B、5 C、6 D、10. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
A、4 B、5 C、6 D、10. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , D为上一点,若是的角平分线,则 .
 12. 如图,在中,以A为圆心,长为半径作弧,交于C,D两点,分别以点C和点D为圆心,大于长为半径作弧,两弧交于点P,作直线 , 交于点E,若 , , 则 .
12. 如图,在中,以A为圆心,长为半径作弧,交于C,D两点,分别以点C和点D为圆心,大于长为半径作弧,两弧交于点P,作直线 , 交于点E,若 , , 则 . 13. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.
13. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.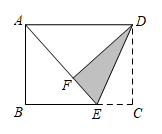 14. 如图,在中,的垂直平分线交于点D . 交于点E . 连接 . 若 , , 则的度数为 .
14. 如图,在中,的垂直平分线交于点D . 交于点E . 连接 . 若 , , 则的度数为 . 15. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.
15. 如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为.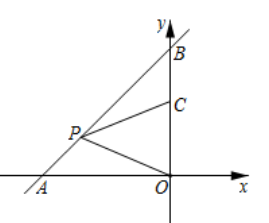 16. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).
16. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).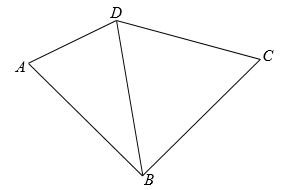
三、解答题
-
17. 如图,在四边形中, , 点在的延长线上,连接 .
 (1)、求证:;(2)、若平分 , 直接写出的形状.18. 如图, , ,点 在 边上, , 和 相交于点 .
(1)、求证:;(2)、若平分 , 直接写出的形状.18. 如图, , ,点 在 边上, , 和 相交于点 .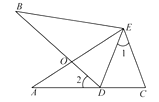 (1)、求证: ≌ ;
(1)、求证: ≌ ;
(2)、若 ,求 的度数.19. 问题:如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC。若∠BAE=90°,∠B=45°,求∠DAC的度数。答案:∠DAC=45°。
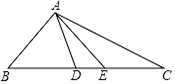
思考:
(1)、如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由。(2)、如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数。20. 如图,在等边三角形ABC中,点M为AB边上任意一点,延长BC至点N,使CN=AM,连接MN交AC于点P,MH⊥AC于点H.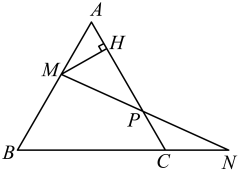 (1)、求证:MP=NP;(2)、若AB=a,求线段PH的长(结果用含a的代数式表示).21. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)、求证:MP=NP;(2)、若AB=a,求线段PH的长(结果用含a的代数式表示).21. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F. (1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.22. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.
(1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.22. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.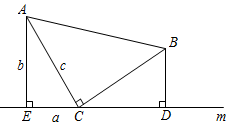
①求证: ;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
23. 如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).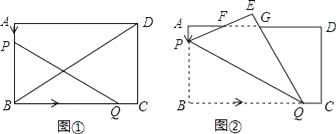 (1)、当t=s时,△BPQ为等腰三角形;(2)、当BD平分PQ时,求t的值;(3)、如图②,将△BPQ沿PQ折叠,点B的对应点为E,PE、QE分别与AD交于点F、G.探索:是否存在实数t,使得AF=EF?如果存在,求出t的值:如果不存在,说明理由.24. 已知△ABC是等腰三角形,AB=AC.
(1)、当t=s时,△BPQ为等腰三角形;(2)、当BD平分PQ时,求t的值;(3)、如图②,将△BPQ沿PQ折叠,点B的对应点为E,PE、QE分别与AD交于点F、G.探索:是否存在实数t,使得AF=EF?如果存在,求出t的值:如果不存在,说明理由.24. 已知△ABC是等腰三角形,AB=AC.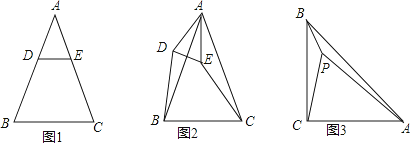 (1)、特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)(2)、发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.(3)、拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
(1)、特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)(2)、发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.(3)、拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.