2024年北师大版数学八年级下册周测卷(第一章第1-2节)基础卷
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
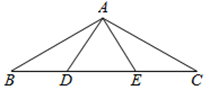
1. 如图,已知等边 , 直线 , 则( )
 A、 B、 C、 D、2. 在等腰三角形中,若 , , 则这个三角形的周长为( )A、21 B、20 C、19 D、18或213. 如图,等边△ABC的两条高AD和BE相交于点O,则∠DOE度数为( )
A、 B、 C、 D、2. 在等腰三角形中,若 , , 则这个三角形的周长为( )A、21 B、20 C、19 D、18或213. 如图,等边△ABC的两条高AD和BE相交于点O,则∠DOE度数为( ) A、60° B、90° C、120° D、150°4. 如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB和AC,当固定点B、C到脚杆E的距离相等,点B、E、C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是 ( )
A、60° B、90° C、120° D、150°4. 如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB和AC,当固定点B、C到脚杆E的距离相等,点B、E、C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是 ( )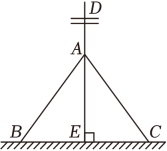 A、等边对等角 B、垂线段最短 C、等腰三角形的三线合一 D、DE是BC的垂直平分线5. 若等腰三角形一个角等于80°,则它的底角是( )A、80° B、50° C、60° D、80°或50°6. 一副三角板如图摆放,则的值是( )
A、等边对等角 B、垂线段最短 C、等腰三角形的三线合一 D、DE是BC的垂直平分线5. 若等腰三角形一个角等于80°,则它的底角是( )A、80° B、50° C、60° D、80°或50°6. 一副三角板如图摆放,则的值是( ) A、125° B、100° C、115° D、105°7. 下列命题是假命题的是( )A、等腰三角形高线、中线和角平分线互相重合 B、全等三角形对应边相等 C、三个角都相等的三角形是等边三角形 D、角平分线上的点到角两边的距离相等8. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、 ,9. 根据图中给定的条件,下列各图中可以判断与一定相等的是( )
A、125° B、100° C、115° D、105°7. 下列命题是假命题的是( )A、等腰三角形高线、中线和角平分线互相重合 B、全等三角形对应边相等 C、三个角都相等的三角形是等边三角形 D、角平分线上的点到角两边的距离相等8. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、 ,9. 根据图中给定的条件,下列各图中可以判断与一定相等的是( )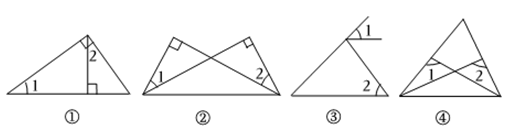 A、 B、 C、 D、10. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、6,8,10 B、7,24,25 C、 , , D、 , ,
A、 B、 C、 D、10. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、6,8,10 B、7,24,25 C、 , , D、 , ,二、填空题
-
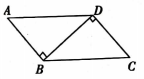
11. 如图,在四边形ABCD中,∠ABD=∠CDB=90°,根据“HL"添加条件可得△ABD≌△CDB .
 12. 如图,已知A,B,D在同一条直线上,∠A=∠CBE=90°,AC=BD,∠1=∠2=35°.则∠D的度数为.
12. 如图,已知A,B,D在同一条直线上,∠A=∠CBE=90°,AC=BD,∠1=∠2=35°.则∠D的度数为. 13. 已知等腰三角形的一个角为70°,则它的顶角为 .14. 如图,在△ABC中,AB=BC=14,D为AB的中点,ED⊥AB,垂足为点D,交BC于点E.若△EAC的周长为24,则AC=.
13. 已知等腰三角形的一个角为70°,则它的顶角为 .14. 如图,在△ABC中,AB=BC=14,D为AB的中点,ED⊥AB,垂足为点D,交BC于点E.若△EAC的周长为24,则AC=. 15. 如图,是的高, . 若 , 则的度数是 .
15. 如图,是的高, . 若 , 则的度数是 .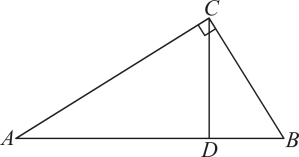 16. 如图,已知OC平分∠AOB,CD∥OB,若OD=6cm,则CD的长为.
16. 如图,已知OC平分∠AOB,CD∥OB,若OD=6cm,则CD的长为.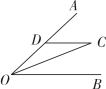
三、解答题
-
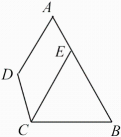
17. 如图,△ECB中,∠CEB=∠B,延长BE至点A,过点A作AD∥CE,∠A=60°,连接CD.
求证:△ECB是等边三角形.
 18. 如图,△ABC中,AB=AC,点D在BC边上,连接AD,若AD=BD,AC=DC,求∠DAC的度数.
18. 如图,△ABC中,AB=AC,点D在BC边上,连接AD,若AD=BD,AC=DC,求∠DAC的度数.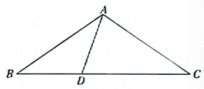 19. 已知:如图,中,是中点,垂足为 , 垂足为 , 且 , 求证:是等腰三角形
19. 已知:如图,中,是中点,垂足为 , 垂足为 , 且 , 求证:是等腰三角形 20. 在一次数学课上,张老师在屏幕上出示了一个例题:
20. 在一次数学课上,张老师在屏幕上出示了一个例题:如图,在△ABC中,D、E分别是AB、AC上的一点,BE与CD交于点O,给出下列四个条件:①BD=CE;②∠BDO=∠CEO;③OB=OC;④∠DBO=∠ECO.要求从这四个等式中选出两个作为已知条件,可判定AB=AC.请写出你的选择,并证明.
 21. 如图,在中, , 点是边上的中点,连结 , 平分交于点 , 过点作交于点 .
21. 如图,在中, , 点是边上的中点,连结 , 平分交于点 , 过点作交于点 . (1)、若 , 求的度数;(2)、求证: .
(1)、若 , 求的度数;(2)、求证: .