【培优卷】2024年浙教版数学七年级下册第1章平行线单元测试

试卷更新日期：2024-02-20 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

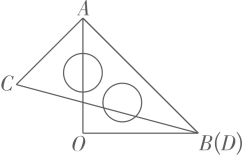
1. 一副三角板按如图所示叠放在一起，其中点 $B$ 、 $D$ 重合，若固定三龟板 $A O B$ ，三角板 $A C D$ 绕点 $A$ 在平面内旋转，当 $∠ B A D =$ （）时， $C D ∥ A B$ ．

A、 $90 °$ B、 $120 °$ 或 $60 °$ C、 $150 °$ 或 $30 °$ D、 $135 °$ 或 $45 °$

查看试题解析
2. 一副直角三角尺叠放如图1所示，现将含 $45^{°}$ 角的三角尺ADE固定不动，将含 $30^{°}$ 角的三角尺ABC绕顶点 $A$ 顺时针转动，使两块三角尺至少有一组边互相平行，如图2，当 $∠ B A D = 15^{°}$ 时， $B C / / D E$ ，则 $∠ B A D (0^{°} <$ $∠ B A D < 180^{°}$ )其他所有可能符合条件的度数为（）

A、 $60^{°}$ 和 $135^{°}$ B、 $45^{°} ， 60^{°} ， 105^{°}$ 和 $135^{°}$ C、 $30^{°}$ 和 $45^{°}$ D、以上都有可能

查看试题解析
3. 如图，∠AOC和∠BOC互补，∠AOB=α ， OM是∠AOC的平分线，ON是∠BOC的平分线，∠MON的度数（）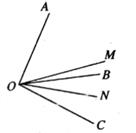

A、180°-2α B、 $\frac{1}{2}$ α C、90°+ $\frac{1}{2}$ α D、90°- $\frac{1}{2}$ α

查看试题解析
4. 如图，AB∥CD，∠EAF=3∠BAF，∠ECF=3∠DCF，则∠E与∠F的数量关系是（）

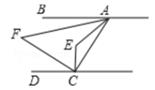A、∠E+∠F=180° B、∠E=3∠F C、∠E-∠F=90° D、∠E=4∠F

查看试题解析
5. 如图，已知AB∥CD，CE，AE分别平分∠ACD，∠CAB，则∠1＋∠2的度数为（）

A、90° B、180° C、120° D、150°

查看试题解析
6. 如图， $A B ∥ C D$ ，将一副直角三角板作如下摆放， $∠ G E F = 60 °$ ， $∠ M N P = 45 °$ ．下列结论：① $G E ∥ M P$ ；② $∠ E F N = 150 °$ ；③ $∠ B E F = 75 °$ ；④ $∠ A E G = ∠ P M N$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，点E在 $A C$ 的延长线上，下列条件中能判断 $A B ∥ C D$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ D + ∠ A C D = 180 °$ C、 $∠ D = ∠ D C E$ D、 $∠ 1 = ∠ 2$

查看试题解析
8. 小明、小亮、小刚、小颖一起研究一道数学题.如图，已知EF⊥AB，CD⊥AB，
小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB.”

小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，

可得到∠CDG=∠BFE.”

小刚说：“∠AGD一定大于∠BFE.”

小颖说：“如果连接GF，则GF一定平行于AB.”

他们四人中，有（）个人的说法是正确的.

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，下列说法错误的是（）

A、因为 $∠ 1 = ∠ 2$ ，所以 $A E ∥ B D$ B、因为 $∠ 3 = ∠ 4$ ，所以 $A B ∥ C D$ C、因为 $∠ 5 = ∠ 1 + ∠ 3$ ，所以 $A E ∥ B D$ D、因为 $∠ 5 = ∠ 2 + ∠ 4$ ，所以 $A E ∥ B D$

查看试题解析
10. 如图，直线 $E F ∥$ 直线 $G H$ ，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，顶点A在 $G H$ 上，顶点B在 $E F$ 上，且 $B A$ 平分 $∠ D B E$ ．若 $∠ C A D = 26 °$ ，求 $∠ B A D$ 的度数．下面是嘉琪在作业本上写出的解答过程，他故意把部分步骤内容用小图标遮挡．

关于小图标遮挡的内容，下面的回答错误的是（）

A、代表 $64 °$ B、代表 $∠ D B E$ C、代表 $\frac{1}{2}$ $∠ D B E$ D、代表 $∠ C B E$

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，将周长为 $20 c m$ 的 $△ A B C$ 沿射线BC方向平移 $2 c m$ 后得到 $△ D E F$ ，则四边形 $A B F D$ 的周长为 $c m$ ．

查看试题解析
12. 在A、B两地之间要修一条公路（如图），从A地测得公路的走向是北偏东60度．如果A、B两地同时开工，那么在B地公路按∠α＝度施工，能使公路准确接通．

查看试题解析
13. 如图， $A E ∥ C F$ ， $∠ A C F$ 的平分线交 $A E$ 于点 $B$ ， $G$ 是 $C F$ 上的一点， $∠ G B E$ 的平分线交 $C F$ 于点 $D$ ，且 $B D ⊥ B C$ ，下列结论：① $B C$ 平分 $∠ A B G$ ；② $A C ∥ B G$ ；③与 $∠ D B E$ 互余的角有 $2$ 个；④若 $∠ A = α$ ，则 $∠ B D F = 180 ° - \frac{α}{2}$ ，其中正确的有．（把你认为正确结论的序号都填上）

查看试题解析
14. 如图是超市里购物车的侧面示意图，扶手AB与车底CD平行，∠2比∠3大10°，∠1是∠2的 $1 \frac{9}{11}$ 倍，则∠2的度数是度．

查看试题解析
15. 如图，两个全等的直角三角形重叠在一起，将其中一个直角三角形沿 $A B$ 的方向平移，平移的距离为线段 $A A^{'}$ 的长，则阴影部分的面积为．

查看试题解析
16. 如图， $A B ∥ C D$ ， $∠ A B C = 40 °$ ， $∠ A C B = 30 °$ ．

(1)、 $∠ A C D =$ ；

(2)、在直线 $C D$ 上取一点 $E$ ，使得 $∠ C A E = ∠ A C B$ ，则 $∠ A E C$ 的度数是．

查看试题解析

三、解答题（共8题，共66分）

17. 根据下列要求画图：

(1)、如图，
点A， B，C分别表示某公园平地上的三棵树，藏宝的地点D与这三棵树恰好构成一个平行四边形，请在图中作出所有可能的藏宝地点D的位置．

(2)、如图，已知点P和∠ABC，以点P为顶点画∠DPE，使得PD∥ BA，PE∥ BC，然用量角器量得：∠ABC=°，∠DPE=°，并猜想∠DPE与∠ABC的关系为．

查看试题解析
18. 如图1是由25个边长为1个单位的小正方形组成的 $5 \times 5$ 网格，三角形 $A B C$ 的端点都在小正方形的顶点，请按要求画图并解决问题：

(1)、将三角形 $A B C$ 向上平移1个单位，向右平移2个单位，画出三角形 $A^{'} B^{'} C^{'}$ ；

(2)、连接 $A A^{'}$ 、 $B B^{'}$ ，则 $A A^{'}$ 与 $B B^{'}$ 之间的数量关系为 ▲ ； $A A^{'}$ 与 $B B^{'}$ 之间的位置关系为 ▲ ；

(3)、如图2，将三角形 $M N P$ 沿 $M M^{'}$ 方向平移若干距离得到三角形 $M^{'} N^{'} P^{'}$ ．若三角形 $M N P$ 和五边形 $M^{'} M N N^{'} P^{'}$ 的周长分别是 $5$ 与 $9$ ，则三角形 $M N P$ 平移的距离为．

查看试题解析
19. 完成下面的说理过程：
已知：如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°.试说明：AB∥CD.
解：∵DE平分∠BDC（已知），
∴∠BDC=2∠1（                 ）
∵BE平分∠ABD（已知），
∴∠ABD=    ▲        （角平分线的定义），
∴∠BDC+∠ABD=2∠1+2∠2=2（∠1+∠2）（等量代换）.
又∵∠1+∠2=90°（已知），
∴∠ABD+∠BDC=    ▲        °（等量代换），
∴AB∥CD（                  ）

查看试题解析
20. 已知一个角的两边与另一个角的两边分别平行，请结合图形，探究这两个角之间的关系，并对你的结论说明理由．

(1)、如图①，AB∥FE，BC∥ED，∠1与∠2的关系是 ▲ ，请说明理由．

(2)、如图②，AB∥FE，BC∥DE，∠1与∠2的关系是 ▲ ，请说明理由．

(3)、经过上述探究，可以得到一个正确的结论：
如果
那么

查看试题解析
21. 如图， $A D ∥ E F$ ， $∠ A E F + ∠ G D C = 180 °$ ． $∠ G D C$ 与 $∠ B A D$ 相等吗？为什么？

查看试题解析
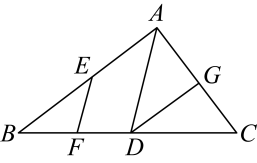22. 如图所示，王飞打算在院子里种上蔬菜，已知院子为东西长32m，南北宽20m的长方形．为了行走方便，要修筑同样宽的三条道路：东西两条，南北一条，南北道路垂直于东西道路，余下的部分要分别种上西红柿、青椒、黄瓜等蔬菜．若每条道路的宽均为1m，则蔬菜的总种植面积是多少？

查看试题解析
23. 如图 $1$ ， $∠ E F H = 90 °$ ，点 $A$ ， $C$ 分别在射线 $F E$ 和 $F H$ 上， $A B / / C D$ ．

(1)、若 $∠ F A B = 150 °$ ，则 $∠ H C D =$ ．

(2)、嘉嘉同学发现：无论 $∠ F A B$ 如何变化， $∠ F A B - ∠ H C D$ 的值始终为定值，并给出了一种证明该发现的辅助线作法如图 $2$ ，过点 $A$ 作 $A M / / F H$ ，交 $C D$ 于点 $M$ ，请你根据嘉嘉同学提供的辅助线，先确定该定值再说明理由．

(3)、如图 $3$ ，把“ $∠ E F H = 90 °$ ”改为“ $∠ E F H = 120 °$ ”，其他条件保持不变，直接写出 $∠ F A B$ 与 $∠ H C D$ 的数量关系．

查看试题解析
24. 【知识背景】在同一平面内，两条直线的位置关系有两种，分别是平行和相交，在相交这种位罟关系中，包括垂直这种特殊位置关系．

(1)、【问题探究】
如图1， $P Q ∥ M N$ ， $A$ ， $B$ 分别在 $P Q$ ， $M N$ 上， $A C$ 平分 $∠ P A B$ 交 $M N$ 于点C ， D是直线 $M N$ 上一点， $A E$ 平分 $∠ B A D$ 交 $M N$ 于点E ．
①若D在点B的右侧，且 $∠ A D C = 30 °$ ， $∠ A E C = 50 °$ ，求 $∠ B A D$ 的度数为 ▲ ．
②如图2，当D在点B的右侧时，过点E作 $E F ⊥ A C$ ，垂足为 $F$ ，记 $∠ A E F = x °$ ， $∠ A D B = y °$ ，直接写出y与x的关系式．

(2)、【拓展应用】
“一带一路”让中国和世界联系更紧密，“中欧班列”为了安全起见在某段铁路两旁安置了A ， B两座可旋转探照灯．如图3，假定主道路是平行的，即 $P Q ∥ M N$ ，连在 $A B$ ，且 $∠ A B N = 45 °$ ．灯 $A$ 发出的射线 $A C$ 自 $A Q$ 顺时针旋转至 $A P$ 便立即回转，灯B发出的射线 $B D$ 自 $B M$ 顺时针旋转至 $B N$ 便立即回转，两灯不停交叉照射巡视．灯A转动的速度是3度/秒，灯B转动的速度是9度/秒，若它们同时开始转动，设转动时间为t秒，在灯A发出的射线 $A C$ 从 $A Q$ 转至 $A P$ 的过程中， $A C$ 与 $B D$ 互相垂直时，请直接写出此时t的值．

查看试题解析

【培优卷】2024年浙教版数学七年级下册第1章平行线 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

【培优卷】2024年浙教版数学七年级下册第1章平行线单元测试