【北师大版·数学】2024年中考二轮复习之圆的综合题
试卷更新日期:2024-02-20 类型:二轮复习
一、选择题
-
1. 如图,已知是直径, , , D是弧的中点,则( )
 A、1 B、2 C、3 D、42. 如图, 内接于圆 , , ,若 ,则弧 的长为( )
A、1 B、2 C、3 D、42. 如图, 内接于圆 , , ,若 ,则弧 的长为( )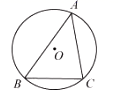 A、 B、 C、 D、3. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为( )
A、 B、 C、 D、3. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为( ) A、4π B、2π C、π D、4. 如图,正五边形内接于 , 连接 , 则( )
A、4π B、2π C、π D、4. 如图,正五边形内接于 , 连接 , 则( )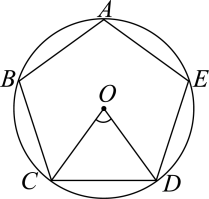 A、 B、 C、 D、5. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )
A、 B、 C、 D、5. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )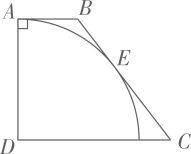 A、 B、 C、 D、6. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( )
A、 B、 C、 D、6. 如图,已知中, , . D、E分别是边、上的点, , 且 . 如果经过点A,且与外切,那么与直线的位置关系是( ) A、相离 B、相切 C、相交 D、不能确定7. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
A、相离 B、相切 C、相交 D、不能确定7. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )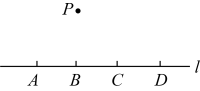 A、3个 B、4个 C、5个 D、6个8. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )
A、3个 B、4个 C、5个 D、6个8. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )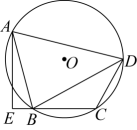 A、3 B、 C、 D、9. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( )
A、3 B、 C、 D、9. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( ) A、8 B、4 C、3.5 D、310. 已知在扇形中, , , 为弧的中点,为半径上一动点,点关于直线的对称点为 , 若点落在扇形内不含边界 , 则长的取值范围是( )
A、8 B、4 C、3.5 D、310. 已知在扇形中, , , 为弧的中点,为半径上一动点,点关于直线的对称点为 , 若点落在扇形内不含边界 , 则长的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm.
 12. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .
12. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .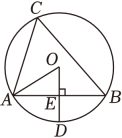 13. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.
13. 如图,在中,直径与弦交于点 . 连接 , 过点的切线与的延长线交于点 . 若 , 则°.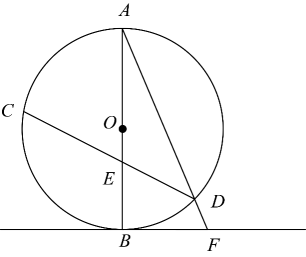 14. 小明对《数书九章》中的“遥度圆城”问题进行了改编:如图,一座圆形城堡有正东、正南、正西和正北四个门,出南门向东走一段路程后刚好看到北门外的一颗大树,向树的方向走9里到达城堡边,再往前走6里到达树下.则该城堡的外围直径为里.
14. 小明对《数书九章》中的“遥度圆城”问题进行了改编:如图,一座圆形城堡有正东、正南、正西和正北四个门,出南门向东走一段路程后刚好看到北门外的一颗大树,向树的方向走9里到达城堡边,再往前走6里到达树下.则该城堡的外围直径为里. 15. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .
15. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .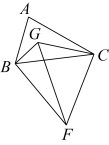
三、作图题
-
16. 如图,由小正方形构成的网格中,每个小正方形的顶点叫做格点,经过A,B,C三个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线,结果用实线).
 (1)、在图1中标出圆心O,并在圆上找一点E,使平分弧;(2)、在图2中的圆上画一点M,使平分.(3)、如图3,的顶点A,B均在格点上,顶点C在网格线上, , P是如图所示的的外接圆上的动点,当时,请用无刻度的直尺,在圆上画出点P.
(1)、在图1中标出圆心O,并在圆上找一点E,使平分弧;(2)、在图2中的圆上画一点M,使平分.(3)、如图3,的顶点A,B均在格点上,顶点C在网格线上, , P是如图所示的的外接圆上的动点,当时,请用无刻度的直尺,在圆上画出点P.四、解答题
-
17. 已知:如图,四边形是的内接四边形,直径交边于点 , 、的延长线相交于点连接 , 若 .
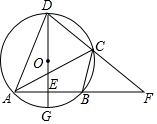 (1)、求证:;(2)、若 , , 求半径.
(1)、求证:;(2)、若 , , 求半径.五、综合题
-
18. 在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请应用此结论.解决以下问题:
如图1,中,().点D是边上的一动点(点D不与B,C重合),将线段绕点A顺时针旋转到线段 , 连接 .
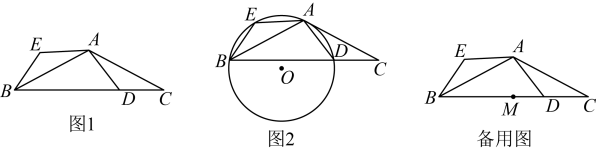 (1)、求证:A,E,B,D四点共圆;(2)、如图2,当时,是四边形的外接圆,求证:是的切线;(3)、已知 , 点M是边的中点,此时是四边形的外接圆,直接写出圆心P与点M距离的最小值.
(1)、求证:A,E,B,D四点共圆;(2)、如图2,当时,是四边形的外接圆,求证:是的切线;(3)、已知 , 点M是边的中点,此时是四边形的外接圆,直接写出圆心P与点M距离的最小值.六、实践探究题
-
19.
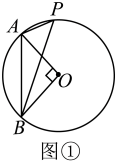
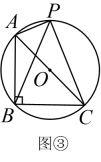 (1)、【感知】如图①,点A、B、P均在上, , 则锐角的大小为度.(2)、【探究】小明遇到这样一个问题:如图②,是等边三角形的外接圆,点P在上(点P不与点A、C重合),连结、、 . 求证: . 小明发现,延长至点E,使 , 连结 , 通过证明 , 可推得是等边三角形,进而得证.
(1)、【感知】如图①,点A、B、P均在上, , 则锐角的大小为度.(2)、【探究】小明遇到这样一个问题:如图②,是等边三角形的外接圆,点P在上(点P不与点A、C重合),连结、、 . 求证: . 小明发现,延长至点E,使 , 连结 , 通过证明 , 可推得是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长至点E,使 , 连结 ,
四边形是的内接四边形,
.
,
.
是等边三角形.
,
请你补全余下的证明过程.
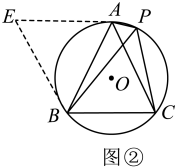
(3)、【应用】如图③,是的外接圆, , 点P在上,且点P与点B在的两侧,连结、、 . 若 , 则的值为 .
-
-
-