吉林省长春市双阳区2023-2024学年九年级上学期期末数学试卷

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，共24分）

1. 若二次根式 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞0 B、x≥﹣3 C、x≥3 D、x≤3

查看试题解析
2. 在平面直角坐标系中，点A（2，3）关于y轴对称的点的坐标是（）

A、（﹣2，﹣3） B、（﹣2，3） C、（2，﹣3） D、（﹣3，﹣2）

查看试题解析
3. 如图，平地上A、B两点被池塘隔开，测量员在岸边选一点C，并分别找到AC和BC的中点D、E，测量得DE=16米，则A、B两点间的距离为（）

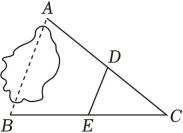A、30米 B、32米 C、36米 D、48米

查看试题解析
4. 如图，在一个直角三角板ABC中， ∠A=60°，则cosA的值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
5. 将抛物线y＝3（x﹣1）²+1向右平移2个单位，再向上平移2个单位，得到抛物线的表达式为（）

A、y＝3（x﹣3）²﹣1 B、y＝3（x+1）²+3 C、y＝3（x+1）²﹣1 D、y＝3（x﹣3）²+3

查看试题解析
6. 如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F．已知AB=2，BC=4，EF=3，则DE的长为（）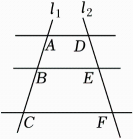

A、1 B、1.5 C、2 D、2.5

查看试题解析
7. 如图，某学习小组为测量学校A与河对岸凉亭B之间的距离，在学校附近选一点C，利用测量仪器测得∠C=90°，∠A=α，AC=4km.据此，可求得学校与凉亭之间的距离AB等于（）

A、4sinαkm B、 $\frac{4}{s i n α} k m$ C、 $\frac{4}{c o s α} k m$ D、4tanαkm

查看试题解析
8. 如图，小明以抛物线为灵感，在平面直角坐标系中设计了一款高OD为13的奖杯，杯体轴截面ABC是抛物线 $y = \frac{4}{7} x^{2} + 6$ 的一部分，则杯口的口径AC长为（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

9. 计算： $\sqrt{2} \times \sqrt{8}$ = .

查看试题解析
10. 若3n＝4m（mn≠0），则 $\frac{n}{m}$ ＝．

查看试题解析
11. 抛物线y＝x²﹣2x+4的顶点坐标是．

查看试题解析
12. 若关于x的一元二次方程x²﹣3x+c＝0有两个不相等的实数根，则c的值可以是 .（写出一个即可）

查看试题解析
13. 南宋数学家杨辉所著《田亩比类乘除捷法》中记载：“直田积八百六十四步，只云长阔共六十步，问长及阔各几步．”译文：一块矩形田地的面积是864平方步，它的长和宽共60步，问它的长和宽各是多少步？设这块矩形田地的长为x步，根据题意可列方程为．

查看试题解析
14. 如图，△ABC与△DEF是位似图形，点O是位似中心，OB：BE=1，若S_△ABC＝2，则S_△DOF＝．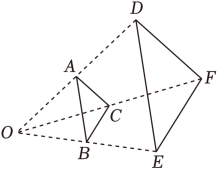

查看试题解析

三、解答题（共78分）

15. 计算 $\sqrt{27} - \sqrt{12} + \sqrt{48}$

查看试题解析
16. 阅读材料，并回答问题．
小明在学习一元二次方程时，解方程2x²﹣8x+5＝0的过程如下：
解：2x²﹣8x+5＝0．
2x²﹣8x＝﹣5．①
$x^{2} - 4 x = - \frac{5}{2}$ ． ②
$x^{2} - 4 x + 4 = - \frac{5}{2} + 4$ ． ③
$(x - 2)^{2} = \frac{3}{2}$ ． ④
$x - 2 = \frac{\sqrt{6}}{2}$ ． ⑤
$x = 2 + \frac{\sqrt{6}}{2}$ ． ⑥
问题：

(1)、上述过程中，从步开始出现了错误（填序号）；

(2)、发生错误的原因是：；

(3)、写出这个方程的解：．

查看试题解析
17. 杭州第19届亚运会吉祥物“江南忆”，具体指A．琮琮、B．宸宸、C．莲莲．如图是三张吉祥物的不透明卡片（卡片除内容外，其余均相同）．将这三张卡片背面朝上洗匀放好，小李同学从这三张卡片中随机抽取一张后，再从剩余的两张卡片中随机抽取一张，请用树状图法或列表法，求两次抽到卡片恰好是琮琮和宸宸的概率．

查看试题解析
18. 抛物线y＝ax²+bx﹣4上部分点的横坐标x，纵坐标y的对应值如下表：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
﹣4
﹣4
0
8
…
根据上表填空或求值：

(1)、抛物线与y轴的交点坐标是；

(2)、求a和b的值；

(3)、当x＝﹣3时，则y的值为．

查看试题解析
19. 某数学实践小组准备测量路灯杆的高度．先从水平地面上一点C处，测得C到路灯杆AB底部B的距离为10米，在C处放置高为1米的测角仪CD，测得路灯杆顶部A的仰角为60°，求路灯杆AB的高度（结果保留根号）．

查看试题解析
20. 如图①、图②、图③均是6×5的正方形网格，每个小正方形的顶点称为格点，且每个小正方形的边长均为1，点A、B、C、D、F、G、K、M、H、N均在格点上．在给定的网格中画图或填空，要求只用无刻度的直尺，保留作图痕迹，不要求写出画法．

(1)、图①中， $\frac{D E}{A E}$ 的值为．

(2)、图②中，在FG上找一点P，使FP＝3．

(3)、图③中，在KM上找一点Q，连接HQ、NQ，使△HKQ∽△NMQ．

查看试题解析
21. 某课外活动小组准备围建一个矩形实践基地，其中一边靠墙，另外三边用长为36米的篱笆围成．已知墙长为19米（如图所示），设这个基地垂直于墙的一边长为x米．

(1)、当矩形实践基地的面积为160平方米时，求垂直于墙的边长x．

(2)、当这个基地的面积最大时，求垂直于墙的边长x，并求这个面积最大值．

查看试题解析
22. 【教材呈现】华师版九年级上册63页例1．
如图，在△ABC中，点D是边AB的三等分点，DE∥BC，DE=5，求BC的长．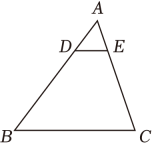

【应用拓展】

(1)、如图①，在△ABC中，点D是边AB的中点，点F为BC延长线上一点，连接DF交AC于点E，若DE：EF=3：1，DG∥AC，EC=2，则AC的长为．

(2)、如图②，在△ABC中，点D为边BA延长线上一点，点E为BC上一点，连接DE交AC于点F，若点A为DB的中点，CE：EB=1：2，△DBE的面积为4，则△CFE（阴影部分）面积为．

查看试题解析
23. 如图，在△ABC中，∠BCA＝90°， AC=8， sinB＝ $\frac{4}{5}$ ，点D是斜边AB的中点，点E是边AC的中点，连接CD，点P为线段CD上一点，作点C关于直线EP对称点F，连结EF、PF，设DP长为x（x＞0）．

(1)、AB的长为．

(2)、求PF长度（用含x的代数式表示）．

(3)、当点F落在直线CD上时，求x的值．

(4)、当直线PF与△ABC的边BC或AC垂直时，直接写出x的值．

查看试题解析
24. 在平面直角坐标系中，抛物线y＝x²+bx﹣3的对称轴为直线x＝1．

(1)、求这条抛物线的解析式．

(2)、当﹣1≤x≤4时，求y的最大值和最小值．

(3)、点P为这条抛物线上的一个动点，点P的横坐标为m（m＞0），以点P为中心作正方形ABCD，AB=2m，且AB⊥x轴．
①当抛物线落在正方形内部的点的纵坐标y随x的增大而减小时，求m的取值范围．
②正方形ABCD的边与抛物线只有两个交点，且交点的纵坐标之差为 $\frac{1}{2}$ 时，直接写出m的值．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	0	﹣4	﹣4	0	8	…