吉林省长春市榆树重点中学2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-02-20 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
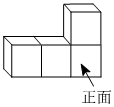
1. 下列各数中,最小的是( )A、-9 B、0 C、-4 D、62. 由个相同的小正方体搭成的几何体如图所示,其主视图是( )
 A、
A、 B、
B、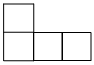 C、
C、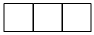 D、
D、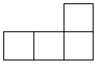 3. 下列选项中与是同类项的是( )A、 B、 C、 D、4. 已知算式5□(-5)的值为0,则“□”内应填入的运算符号为( )A、+ B、- C、× D、÷5. 如图,某村庄要在河岸上建一个水泵房引水到处.他们的做法是:过点作于点D,将水泵房建在了D处,这样做最节省水管长度,其数学道理是( )
3. 下列选项中与是同类项的是( )A、 B、 C、 D、4. 已知算式5□(-5)的值为0,则“□”内应填入的运算符号为( )A、+ B、- C、× D、÷5. 如图,某村庄要在河岸上建一个水泵房引水到处.他们的做法是:过点作于点D,将水泵房建在了D处,这样做最节省水管长度,其数学道理是( )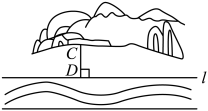 A、两点确定一条直线 B、垂线段最短 C、两点之间,线段最短 D、过一点有且仅有一条直线与已知直线垂直6. 下列说法错误的是( )A、是二次三项式 B、的系数是 C、的次数是 D、的常数项是7. 如图,地和地都是海上观测站,地在灯塔的北偏东方向, , 则地在灯塔的( )
A、两点确定一条直线 B、垂线段最短 C、两点之间,线段最短 D、过一点有且仅有一条直线与已知直线垂直6. 下列说法错误的是( )A、是二次三项式 B、的系数是 C、的次数是 D、的常数项是7. 如图,地和地都是海上观测站,地在灯塔的北偏东方向, , 则地在灯塔的( )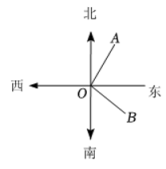 A、南偏东方向 B、南偏东方向 C、南偏西方向 D、东偏南方向8. 如图,下列条件中能判定是( )
A、南偏东方向 B、南偏东方向 C、南偏西方向 D、东偏南方向8. 如图,下列条件中能判定是( )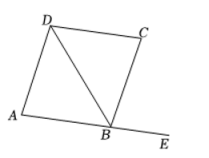 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
9. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为.10. 某种商品原价每件元,现打折出售,这时的售价是元.11. 若 , 则的补角为 .12. 一节数学实践课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD , 并要说出自己做法的依据.小奇、小妙两位同学的做法如图:小奇说:“我做法的依据是:同位角相等,两直线平行.”则小妙做法的依据是.
 13. 如图是一个正方体的展开图,把它折叠成正方体后,与“有”字所在面相对的面上的字是.
13. 如图是一个正方体的展开图,把它折叠成正方体后,与“有”字所在面相对的面上的字是.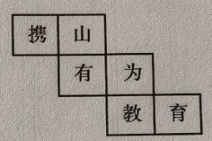 14. 如图, , 平分 , 若 , 则度.
14. 如图, , 平分 , 若 , 则度.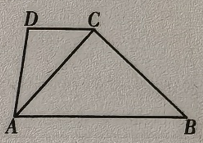
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
-
15. 计算: .16. 先化简,再求值: , 其中 , .17. 已知 .(1)、化简;(2)、若 , 且与的和不含的一次项,求的值.18. 如图,直线 , 相交于点O, .
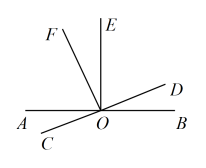 (1)、写出的所有余角;(2)、若 , 求的度数.19. 现规定一种新运算,规则如下: , 例如: .(1)、按照这个规则, .(2)、按照这个规则,先化简 , 并计算当 , 时,的值.20. 如图,某公园有一块长为米,宽为米的长方形土地,现将三面留出宽都是米的小路,余下的部分设计成花圃种植名贵花草,并用篱笆把四周围起来.
(1)、写出的所有余角;(2)、若 , 求的度数.19. 现规定一种新运算,规则如下: , 例如: .(1)、按照这个规则, .(2)、按照这个规则,先化简 , 并计算当 , 时,的值.20. 如图,某公园有一块长为米,宽为米的长方形土地,现将三面留出宽都是米的小路,余下的部分设计成花圃种植名贵花草,并用篱笆把四周围起来.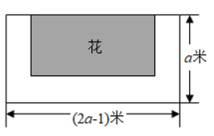 (1)、用代数式表示所用篱笆的总长度;(2)、当 , 时,求所用篱笆的总长度.21. 如图,于点P , ∠1+∠2=90°.
(1)、用代数式表示所用篱笆的总长度;(2)、当 , 时,求所用篱笆的总长度.21. 如图,于点P , ∠1+∠2=90°.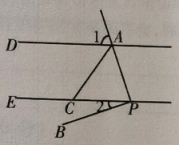 (1)、判断直线AD与PE的位置关系,并说明理由;(2)、若AC平分 , 交PE于点C , 且 , 求∠2的度数.22. 如图,、、、四点在同一直线上.
(1)、判断直线AD与PE的位置关系,并说明理由;(2)、若AC平分 , 交PE于点C , 且 , 求∠2的度数.22. 如图,、、、四点在同一直线上. (1)、若 .
(1)、若 .比较线段的大小: 填“”“”或“=”;
若 , 且 , 的长;
(2)、若线段被点、分成了::三部分,且 , 点是的中点,直接写出的长.23. 如图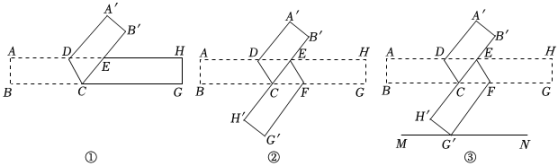 (1)、【知识初探】
(1)、【知识初探】如图 , 在长方形纸条中, , , 将长方形纸条沿折叠,点落在处,点落在处,交于点若 , 则 度;
(2)、【类比再探】如图 , 在图的基础上将四边形折叠,点落在直线上的处,点落在处,得到折痕 , 则折痕与有怎样的位置关系?说明理由;
(3)、【拓展延伸】如图 , 在图的基础上,过点作的平行线 , 请你直接写出和的数量关系,不用说明理由.
24. 将一副直角三角板如图摆放在直线上直角三角板和直角三角板 , , , , , 保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转.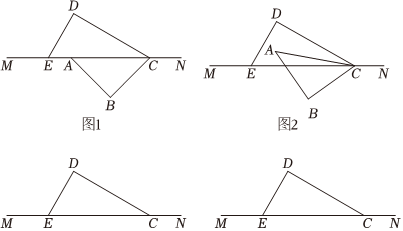 (1)、如图 , 当为的角平分线时, .(2)、当时,求的度数?(3)、在旋转过程中,当三角板的边平行于三角板的某一边时不包含重合的情形 , 求此时的值为 直接写出答案即可
(1)、如图 , 当为的角平分线时, .(2)、当时,求的度数?(3)、在旋转过程中,当三角板的边平行于三角板的某一边时不包含重合的情形 , 求此时的值为 直接写出答案即可