重庆市铜梁区重点中学2023-2024学年九年级上学期数学月考考试试卷
试卷更新日期:2024-02-20 类型:月考试卷
一、选择题(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、
-
1. 下列函数中,是二次函数的是( )A、 B、 C、y=8x2+1 D、y=x2﹣(x﹣3)22. 用公式法解一元二次方程3x2=2x﹣3时,首先要确定a、b、c的值,下列叙述正确的是( )A、a=3,b=2,c=3 B、a=﹣3,b=2,c=3 C、a=3,b=2,c=﹣3 D、a=3,b=﹣2,c=33. 将抛物线y=(x﹣1)2+2先向右平移2个单位长度,再向下平移3个单位长度,得到抛物线的顶点坐标是( )A、(﹣1,5) B、(﹣1,﹣1) C、(3,﹣1) D、(3,5)4. 根据下列表格中二次函数y=ax2+bx+c的自变量x与y的对应值,判断关于x的一元二次方程ax2+bx+c=0的一个解的大致范围是( )
x
﹣1
0
1
2
3
4
y
﹣7
﹣5
﹣1
5
13
23
A、1<x<2 B、﹣1<x<1 C、﹣7<x<﹣1 D、﹣1<x<55. 若点A(﹣3,y1),B(1,y2),C(2,y3)是抛物线y=﹣x2+1上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y2>y1>y3 C、y2>y3>y1 D、y3>y2>y16. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )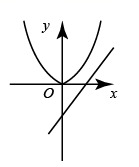 A、
A、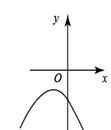 B、
B、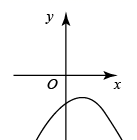 C、
C、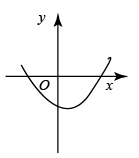 D、
D、 7. 从前,有一个醉汉拿着竹竿进屋,横拿竖拿都拿不进去,横着比门框宽4尺,竖着比门框高2尺.另一醉汉叫他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,你知道竹竿有多长吗?若设竹竿的长为x尺,则下列方程,满足题意的是( )A、x2+(x﹣2)2=(x﹣4)2 B、(x﹣4)2+(x﹣2)2=x C、(x﹣4)2+(x﹣2)2=x2 D、x2+(x﹣4)2=(x﹣2)28. 如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣4,0)和原点.下列说法正确的是( )
7. 从前,有一个醉汉拿着竹竿进屋,横拿竖拿都拿不进去,横着比门框宽4尺,竖着比门框高2尺.另一醉汉叫他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,你知道竹竿有多长吗?若设竹竿的长为x尺,则下列方程,满足题意的是( )A、x2+(x﹣2)2=(x﹣4)2 B、(x﹣4)2+(x﹣2)2=x C、(x﹣4)2+(x﹣2)2=x2 D、x2+(x﹣4)2=(x﹣2)28. 如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣4,0)和原点.下列说法正确的是( ) A、abc>0 B、4ac﹣b2>0 C、3a﹣b<0 D、5a+c<09. 如图,在正方形ABCD中,E是边AD中点,F是边AB上一动点,G是EF延长线上一点,且GF=EF . 若AD=4,则EG2+CG2的最小值为( )
A、abc>0 B、4ac﹣b2>0 C、3a﹣b<0 D、5a+c<09. 如图,在正方形ABCD中,E是边AD中点,F是边AB上一动点,G是EF延长线上一点,且GF=EF . 若AD=4,则EG2+CG2的最小值为( ) A、52 B、60 C、68 D、7610. 已知函数f(x)=x2+2x , g(x)=2x2+6x+n2+3,当x=1时,f(1)=12+2×1=3,g(1)=2+6+n2+3=n2+11.则以下结论正确的有( )
A、52 B、60 C、68 D、7610. 已知函数f(x)=x2+2x , g(x)=2x2+6x+n2+3,当x=1时,f(1)=12+2×1=3,g(1)=2+6+n2+3=n2+11.则以下结论正确的有( )①若函数g(x)的顶点在x轴上,则;
②无论x取何值,总有g(x)>f(x);
③若﹣1≤x≤1时,g(x)+f(x)的最小值为7,则n=±3;
④当n=1时,令 , 则h(1)•h(2)…h(2023)=2024.
A、1个 B、2个 C、3个 D、4个二、填空题(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.
-
11. 若二次函数y=x2﹣bx+b﹣2的图象经过原点,则b= .12. 如图是一个计算程序,当输出值y=100时,输入x的值为 .
 13. 若一元二次方程x2﹣3x﹣1=0的两根分别为x1、x2 , 则 = .14. 如图,抛物线y=﹣x2+bx+c交y轴于点(0,5),对称轴为直线x=﹣2,若y≥5,则x的取值范围是 .
13. 若一元二次方程x2﹣3x﹣1=0的两根分别为x1、x2 , 则 = .14. 如图,抛物线y=﹣x2+bx+c交y轴于点(0,5),对称轴为直线x=﹣2,若y≥5,则x的取值范围是 . 15. 如图,图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m , 水面宽4m , 如图(2)建立平面直角坐标系,当水面下降0.5m时,水面宽增加 m .
15. 如图,图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m , 水面宽4m , 如图(2)建立平面直角坐标系,当水面下降0.5m时,水面宽增加 m . 16. 如果关于x的分式方程有整数解,且二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么符合条件的所有整数m的和为 .17. 一个四位数n , 如果千位与十位上的数字之和等于百位与个位上的数字之和,则称n为“等和数”,将这个“等和数”反序排列(即千位与个位对调,百位与十位对调)得到一个新的四位数m , 记 , 则D(1254)=;若某个“等和数”n的千位与十位上的数字之和为8,D(n)为正数且能表示为两个连续偶数的平方差,则满足条件的最大“等和数”n是 .
16. 如果关于x的分式方程有整数解,且二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么符合条件的所有整数m的和为 .17. 一个四位数n , 如果千位与十位上的数字之和等于百位与个位上的数字之和,则称n为“等和数”,将这个“等和数”反序排列(即千位与个位对调,百位与十位对调)得到一个新的四位数m , 记 , 则D(1254)=;若某个“等和数”n的千位与十位上的数字之和为8,D(n)为正数且能表示为两个连续偶数的平方差,则满足条件的最大“等和数”n是 .三、解答题(本大题共8个小题,19题8分,其它各题每小题8分,共78分)解答题时每小题必须给出
-
18. 在学习等边三角形的过程中,小睿同学发现一个规律:在等边△ABC中,点D是AB边上任意一点,连接CD , 过点A的射线AE交BC于点E , 交CD于点F , 当∠BAE=∠ACD时,则必有BD=CE . 为验证此规律的正确性,小睿的思路是:先利用图,作∠BAE=∠ACD , 再通过证全等得出结论.请根据小睿的思路完成以下作图与填空:
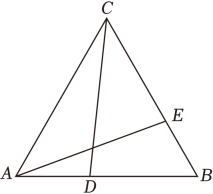 (1)、用直尺和圆规在图的基础上作∠BAE=∠ACD , AE交BC于点E , 交CD于点F . (不写作法,不下结论,只保留作图痕迹)(2)、证明:∵△ABC为等边三角形
(1)、用直尺和圆规在图的基础上作∠BAE=∠ACD , AE交BC于点E , 交CD于点F . (不写作法,不下结论,只保留作图痕迹)(2)、证明:∵△ABC为等边三角形∴AC=AB=BC , ( ) ①
在△ACD和△BAE中
∴△ACD≌△BAE(ASA)
∴ ▲ ③
又∵AB=BC
∴AB﹣AD= ▲ ④
∴BD=CE .
19. 解方程:(1)、x2﹣4x=7;(2)、3x(3x+1)=6x+2.20. 巴川中学STEAM创新教育学部为提高学生的安全意识和安全技能,组织七、八年级学生进入区消防支队进行了实地学习和体验,并在学习结束后开展了一次消防知识竞赛.成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分.学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:年级
平均分
中位数
众数
方差
七年级
8.76
a
9
1.06
八年级
8.76
8
b
1.38
 (1)、根据以上信息可以求出:a= , b= , 并把七年级竞赛成绩统计图补充完整;(2)、依据数据分析表,你认为七年级和八年级哪个年级的成绩更好,并说明理由;(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人?21. 重庆中国三峡博物馆(重庆博物馆)是一座集巴渝文化、三峡文化、抗战文化、移民文化和城市文化等为特色的历史艺术类综合性博物馆,也是国家4A级风景名胜区.每到假期各地游客纷纷前来游玩.据统计,今年国庆小长假第一天的游客人数为5000人次,第三天游客人数达到6050人次.(1)、求今年国庆小长假第一天至第三天游客人数的平均日增长率;(2)、博物馆附近某商店推出了木质旅游扇,每把扇子的成本为6元.根据销售经验,每把扇子定价为25元时,平均每天可售出300把.若每把扇子的售价每降价1元,平均每天可多售出20把.设每把扇子降价x元,商店每天所获利润为w元,求每把扇子的定价为多少元时,商店每天所获利润最大?最大利润是多少元?22. 如图,在矩形ABCD中,AB=3,BC=4,点P从点B出发,沿折线B﹣C﹣D﹣A运动,当点P运动到点A时停止运动.设点P运动路程为x , △ABP的面积为y ,
(1)、根据以上信息可以求出:a= , b= , 并把七年级竞赛成绩统计图补充完整;(2)、依据数据分析表,你认为七年级和八年级哪个年级的成绩更好,并说明理由;(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人?21. 重庆中国三峡博物馆(重庆博物馆)是一座集巴渝文化、三峡文化、抗战文化、移民文化和城市文化等为特色的历史艺术类综合性博物馆,也是国家4A级风景名胜区.每到假期各地游客纷纷前来游玩.据统计,今年国庆小长假第一天的游客人数为5000人次,第三天游客人数达到6050人次.(1)、求今年国庆小长假第一天至第三天游客人数的平均日增长率;(2)、博物馆附近某商店推出了木质旅游扇,每把扇子的成本为6元.根据销售经验,每把扇子定价为25元时,平均每天可售出300把.若每把扇子的售价每降价1元,平均每天可多售出20把.设每把扇子降价x元,商店每天所获利润为w元,求每把扇子的定价为多少元时,商店每天所获利润最大?最大利润是多少元?22. 如图,在矩形ABCD中,AB=3,BC=4,点P从点B出发,沿折线B﹣C﹣D﹣A运动,当点P运动到点A时停止运动.设点P运动路程为x , △ABP的面积为y , (1)、直接写出y1与x的函数关系,并注明x的取值范围;(2)、在给出的平面直角坐标系中画出y1的函数图象,并写出它的一条性质;(3)、函数y2=x2﹣8x+17的图象如图所示,请利用图象,直接写出当y1=y2时,自变量x的值.(结果精确到0.1,误差不超过0.2)23. 今年贵州榕江村超爆火出圈,全国各地足球爱好者闻讯而至.在某一场足球比赛中,进攻方甲队三名球员A、C、D , 与乙队的防守球员B的位置如图所示.此时足球在球员A脚下,他想将球绕过对手B传至队友D处,再由D经线路DC回传给队友C . 已知对手B在A的北偏东60°方向,AB=12米.球员C在对手B的正东方向,BC=3米.球员D在队友C的正北方向,且在队友A的北偏东30°方向.(参考数据:≈1.73)
(1)、直接写出y1与x的函数关系,并注明x的取值范围;(2)、在给出的平面直角坐标系中画出y1的函数图象,并写出它的一条性质;(3)、函数y2=x2﹣8x+17的图象如图所示,请利用图象,直接写出当y1=y2时,自变量x的值.(结果精确到0.1,误差不超过0.2)23. 今年贵州榕江村超爆火出圈,全国各地足球爱好者闻讯而至.在某一场足球比赛中,进攻方甲队三名球员A、C、D , 与乙队的防守球员B的位置如图所示.此时足球在球员A脚下,他想将球绕过对手B传至队友D处,再由D经线路DC回传给队友C . 已知对手B在A的北偏东60°方向,AB=12米.球员C在对手B的正东方向,BC=3米.球员D在队友C的正北方向,且在队友A的北偏东30°方向.(参考数据:≈1.73) (1)、求传球线路CD的长(结果精确到1米);(2)、根据对手B的跑动和拦截范围估计,对手B可以破坏掉在B点5米范围内的球.球员D经线路DC传球给队友C的同时,队友C沿CD方向去接球,已知球速为10m/s , 球员C的平均速度为5m/s . 计算说明球员C是否能避开防守顺利接到球?24. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)和点B , 与y轴正半轴交于点C , 且OC=OB .
(1)、求传球线路CD的长(结果精确到1米);(2)、根据对手B的跑动和拦截范围估计,对手B可以破坏掉在B点5米范围内的球.球员D经线路DC传球给队友C的同时,队友C沿CD方向去接球,已知球速为10m/s , 球员C的平均速度为5m/s . 计算说明球员C是否能避开防守顺利接到球?24. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)和点B , 与y轴正半轴交于点C , 且OC=OB . (1)、求该抛物线的函数表达式;(2)、点P为直线BC上方该抛物线上任意一点,过点P作PFlly轴交BC于点F , 作PE⊥BC于点E , 当PF的值最大时,求点P的坐标,并求出此时PF+PE的最大值;(3)、如图2,在(2)问的条件下,将该抛物线沿射线CB的方向平移个单位后得到新抛物线y' , 新抛物线y'与原抛物线的交点为M . 在新抛物线y'的对称轴上有一点N , 在平面内有一点K , 是否存在以点P , K , M , N为顶点的四边形是以PN为边的菱形?若存在,请直接写出点K的坐标并写出求解K点坐标的其中一种情况的过程;若不存在,请说明理由.25. 已知△ABC是等腰直角三角形,∠ACB=90°,CA=CB , 点D在线段AB上运动.
(1)、求该抛物线的函数表达式;(2)、点P为直线BC上方该抛物线上任意一点,过点P作PFlly轴交BC于点F , 作PE⊥BC于点E , 当PF的值最大时,求点P的坐标,并求出此时PF+PE的最大值;(3)、如图2,在(2)问的条件下,将该抛物线沿射线CB的方向平移个单位后得到新抛物线y' , 新抛物线y'与原抛物线的交点为M . 在新抛物线y'的对称轴上有一点N , 在平面内有一点K , 是否存在以点P , K , M , N为顶点的四边形是以PN为边的菱形?若存在,请直接写出点K的坐标并写出求解K点坐标的其中一种情况的过程;若不存在,请说明理由.25. 已知△ABC是等腰直角三角形,∠ACB=90°,CA=CB , 点D在线段AB上运动. (1)、如图1,连接CD , 过点C作CE⊥CD交BA的延长线于点E . 过点A作AF⊥AB交CE于点F , 若BD=2,EA=3,求EF的长;(2)、如图2,点H是BC边上一点,连接DH , 过点A作AG∥BC交HD延长线于点G . 若BH=AG , 将AD绕点D顺时针旋转60°得到线段MD , MD交AC于点K , 连接AM , 过点C作CN⊥MD交AM于点N , 垂足为P . 求证:MN+MC=MD;(3)、如图3,若AB=4,连接CD并将CD绕点D逆时针旋转90°得到线段QD , 连接CQ、BQ , 取CQ中点T , 点R在AC上且AC=4CR , 连接RT , 直接写出当RT+QB取得最小值时△BDQ的面积.
(1)、如图1,连接CD , 过点C作CE⊥CD交BA的延长线于点E . 过点A作AF⊥AB交CE于点F , 若BD=2,EA=3,求EF的长;(2)、如图2,点H是BC边上一点,连接DH , 过点A作AG∥BC交HD延长线于点G . 若BH=AG , 将AD绕点D顺时针旋转60°得到线段MD , MD交AC于点K , 连接AM , 过点C作CN⊥MD交AM于点N , 垂足为P . 求证:MN+MC=MD;(3)、如图3,若AB=4,连接CD并将CD绕点D逆时针旋转90°得到线段QD , 连接CQ、BQ , 取CQ中点T , 点R在AC上且AC=4CR , 连接RT , 直接写出当RT+QB取得最小值时△BDQ的面积.