湖南省衡阳市衡阳县五校联考2023-2024学年九年级上学期第三次月考数学试题

试卷更新日期：2024-02-20 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共36分）

1. 要使式子 $\frac{\sqrt{x + 1}}{x}$ 有意义， $x$ 的取值范围是（）

A、 $x \neq - 1$ B、 $x \neq 0$ C、 $x > - 1$ 且 $\neq 0$ D、 $x \geq - 1$ 且 $x \neq 0$

查看试题解析
2. 三角形两边长分别为3和6，第三边的长是方程 $x^{2} - 13 x + 36 = 0$ 的两根，则该三角形的周长为（）

A、13 B、15 C、18 D、13或18

查看试题解析
3. 如图，在▱ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S_△_DEF：S_△_ABF=4：25，则DE：EC=（）

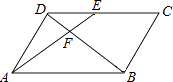A、2：5 B、2：3 C、3：5 D、3：2

查看试题解析
4. 锐角 $α$ 满足 $s i n α > \frac{\sqrt{2}}{2}$ ，且 $t a n α < \sqrt{3}$ ，则 $α$ 的取值范围为（）

A、 $3 0^{∘} < α < 4 5^{∘}$ B、 $4 5^{∘} < α < 6 0^{∘}$ C、 $6 0^{∘} < α < 9 0^{∘}$ D、 $3 0^{∘} < α < 6 0^{∘}$

查看试题解析
5. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球，这些球除颜色外完全相同，其中有5个黄球，4个蓝球．若随机摸出一个蓝球的概率为 $\frac{1}{3}$ ，则随机摸出一个红球的概率为（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{5}{12}$ D、 $\frac{1}{2}$

查看试题解析
6. 将抛物线 $y = x^{2} - 2 x + 3$ 向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（）

A、 $y = {(x - 1)}^{2} + 4$ B、 $y = {(x - 4)}^{2} + 4$ C、 $y = {(x + 2)}^{2} + 6$ D、 $y = {(x - 4)}^{2} + 6$

查看试题解析
7. 当 $| a | = - a$ 时， $| 2 a - \sqrt{a^{2}} | =$ （）

A、 $a$ B、 $- a$ C、 $3 a$ D、 $- 3 a$

查看试题解析
8. 若关于x的方程 $k x^{2} - 3 x - \frac{9}{4} = 0$ 有实数根，则实数k的取值范围是（）

A、 $k = 0$ B、 $k \geq - 1$ 且 $k \neq 0$ C、 $k \geq - 1$ D、 $k > - 1$

查看试题解析
9. 如图，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD=2OA=6，AD：AB=3：1，则点C的坐标是（）

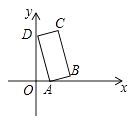A、（2，7） B、（3，7） C、（3，8） D、（4，8）

查看试题解析
10. 如图，在 $△ A B C$ 中， $A C ⊥ B C$ ， $∠ A B C = 3 0^{∘}$ ，点 $D$ 是 $C B$ 延长线上的一点，且 $B D = B A$ ，则 $t a n ∠ D A C$ 的值为（）

A、 $2 + \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 + \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
11. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 1$ ，给出下列结论：① $b^{2} = 4 a c$ ；② $a b c > 0$ ；③ $a > c$ ；④ $4 a - 2 b + c > 0$ ，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，垂直于x轴的直线AB分别与抛物线C₁：y=x²（x≥0）和抛物线C₂：y= $\frac{x^{2}}{4}$ （x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C₂交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C₁交于点E，F，则 $\frac{S_{△ O F B}}{S_{△ E A D}}$ 的值为（）

A、 $\frac{\sqrt{2}}{6}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题（每小题3分，共18分）

13. 已知 $x$ ， $y$ 为实数，且 $y = \sqrt{x^{2} - 9} - \sqrt{9 - x^{2}} + 4$ ，则 $x - y$ 的值为.

查看试题解析
14. 在 $△ A B C$ 中 $B C = 2$ ， $A B = 2 \sqrt{3}$ ， $A C = b$ ，且关于 $x$ 的方程 $x^{2} - 4 x + b = 0$ 有两个相等的实数根，则 $A C$ 边上的中线长为.

查看试题解析
15. 如图，在边长为3的菱形ABCD中，点E在边CD上，点F为BE延长线与AD延长线的交点．若DE=1，则DF的长为．

查看试题解析
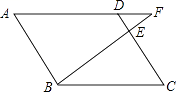16. 在▱ABCD中，对角线AC，BD相交于点O，若AB=4，BD=10，sin∠BDC= $\frac{3}{5}$ ，则▱ABCD的面积是．

查看试题解析
17. 已知函数 $y = - {(x - 1)}^{2}$ 图象上两点 $A (2 ， y_{1})$ ， $B (a ， y_{2})$ ，其中 $a > 2$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是 $y_{1}$ $y_{2}$ （填“＜”、“＞”或“＝”）

查看试题解析
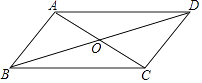18.
如图，已知动点A在函数 $y = \frac{4}{x} (x > 0)$ 的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC．直线DE分别交x，y轴分别于点P，Q．当QE：DP=4：9时，图中阴影部分的面积等于．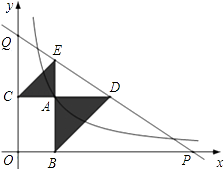

查看试题解析

三、解答题（19～21题每小题6分，22～23每小题8分，24～25每小题10分，26题12分，共66分）

19. 化简： $\frac{2}{3} \sqrt{9 x} + 6 \sqrt{\frac{x}{4}} - 2 x \sqrt{\frac{1}{x}}$ ，并将你所喜欢的 $x$ 值代入化简结果进行计算.

查看试题解析
20. 关于x的一元二次方程 $x^{2} - (k + 3) x + 2 k + 2 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程有一个根小于1，求k的取值范围.

查看试题解析
21. 已知：如图， $△ A B C$ 中， $A B = A C$ ， $A D$ 是中线， $P$ 是 $A D$ 上一点，过 $C$ 作 $C F ∥ A B$ ，延长 $B P$ 交 $A C$ 于 $E$ ，交 $C F$ 于 $F$ ，求证： $B P^{2} = P E \cdot P F$ .

查看试题解析
22. 如图所示，我国两艘海监船 $A$ ， $B$ 在南海海域巡航，某一时刻，两船同时收到指令，立即前往救援遇险抛锚的渔船 $C$ ，此时， $B$ 船在 $A$ 船的正南方向5海里处， $A$ 船测得渔船 $C$ 在其南偏东45°方向， $B$ 船测得渔船 $C$ 在其南偏东53°方向，已知 $A$ 船的航速为30海里/小时， $B$ 船的航速为25海里/小时，问 $C$ 船至少要等待多长时间才能得到救援?（参考数据： $s i n 5 3^{∘} \approx \frac{4}{5}$ ， $c o s 5 3^{∘} \approx \frac{3}{5}$ ， $t a n 5 3^{∘} \approx \frac{4}{3}$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
23. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2}$ ， $\frac{1}{4}$ ， 1的卡片，乙同学手中藏有三张分别标1，3，2的卡片，卡片外形相同.现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为 $a$ ， $b$ .

(1)、请你用树形图或列表法列出所有可能的结果.

(2)、现制定这样一个游戏规则：若所选出的 $a$ ， $b$ 能使得 $a x^{2} + b x + 1 = 0$ 有两个不相等的实数根，则称甲获胜；否则称乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释.

查看试题解析
24. 为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量 $y$ （件）与销售单价 $x$ （元）之间的关系近似满足一次函数： $y = - 10 x + 500$ .

(1)、李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元?

(2)、设李明获得的利润为 $w$ （元），当销售单价定为多少元时，每月可获得最大利润?

(3)、物价部门规定，这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元?

查看试题解析
25. 在锐角 $△ A B C$ 中，点 $D$ 、 $E$ 分别在 $A C$ 、 $A B$ 上， $A G ⊥ B C$ 于点 $G$ ， $A F ⊥ D E$ 于 $F$ ， $∠ E A F = ∠ G A C$ .

(1)、求证： $△ A D E ∽ △ A B C$ ；

(2)、若 $A D = 3$ ， $A B = 5$ ，求 $\frac{A F}{A G}$ 的值.

查看试题解析
26. 如图，抛物线经过点 $A (1 ， 0)$ ， $B (5 ， 0)$ ， $C (0 ， \frac{10}{3})$ 三点，设点 $E (x ， y)$ 是抛物线上一动点，且在 $x$ 轴下方，四边形 $O E B F$ 是以 $O B$ 为对角线的平行四边形.
备用图

(1)、求抛物线的解析式；

(2)、当点 $E (x ， y)$ 运动时，试求平行四边形 $O E B F$ 的面积 $S$ 与 $x$ 之间的函数关系式，并求出面积 $S$ 的最大值

(3)、是否存在这样的点 $E$ ，使平行四边形 $O E B F$ 为正方形?若存在，求 $E$ 点， $F$ 点的坐标；若不存在，请说明理由.

查看试题解析