贵州省铜仁市碧江区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、单选题（每小题3分，共36分，每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置填涂）

1. 现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数中属于无理数的是（）

A、 $\frac{2}{5}$ B、 $- \sqrt{9}$ C、0 D、 $\sqrt{8}$

查看试题解析
3. 若一个三角形的两边长分别为4和9，则第三边长可能是（）

A、3 B、4 C、5 D、11

查看试题解析
4. $2023$ 年 $9$ 月 $9$ 日，上海微电子研发的 $28 n m$ 浸没式光刻机的成功问世，标志着我国在光刻机领域迈出了坚实的一步．已知 $28 n m$ 为 $0.000000028$ 米，数据 $0.000000028$ 用科学记数法表示为（）

A、 $2.8 \times 1 0^{- 10}$ B、 $2.8 \times 1 0^{- 8}$ C、 $2.8 \times 1 0^{- 6}$ D、 $2.8 \times 1 0^{- 9}$

查看试题解析
5. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $2 a^{2} \cdot a^{3} = 2 a^{6}$ C、 $a^{6} \div a^{2} = a^{4}$ D、 $(- 2 a)^{- 2} = 4 a^{2}$

查看试题解析
6. 下列命题是真命题的是（）

A、相等的两个角是对顶角 B、同位角相等 C、如果 $a ∥ c$ ， $b ∥ c$ ，那么 $a ∥ b$ D、如果 $a ⊥ c$ ， $b ⊥ c$ ，那么 $a ∥ b$

查看试题解析
7. 实数a ， b ， c在数轴上如图所示，则下列选项中的式子不成立的是（）

A、 $a b > 0$ B、 $a c < b c$ C、 $a b < b c$ D、 $b c < 0$

查看试题解析
8. 若关于x的方程 $\frac{x + 2}{x + 3} = \frac{m}{x + 3}$ 无解，则m的值为 $($ 　　 $)$

A、 $m = 1$ B、 $m = - 1$ C、 $m = 2$ D、 $m = - 2$

查看试题解析
9. 阅读以下作图步骤：
①在 $O A$ 和 $O B$ 上分别截取 $O C ， O D$ ，使 $O C = O D$ ；②分别以 $C ， D$ 为圆心，以大于 $\frac{1}{2} C D$ 的长为半径作弧，两弧在 $∠ A O B$ 内交于点 $M$ ；③作射线 $O M$ ，连接 $C M ， D M$ ，如图所示．根据以上作图，一定可以推得的结论是（）

A、 $∠ 1 = ∠ 2$ 且 $C M = D M$ B、 $∠ 1 = ∠ 3$ 且 $C M = D M$ C、 $∠ 1 = ∠ 2$ 且 $O D = D M$ D、 $∠ 2 = ∠ 3$ 且 $O D = D M$

查看试题解析
10. 一次数学活动中，小明对纸带沿AB折叠，量得 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
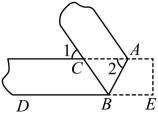11. 我市某区为30万人接种新冠疫苗，由于市民积极配合这项工作，实际每天接种人数是原计划的1.2倍，结果提前20天完成了这项工作．设原计划每天接种 $x$ 万人，根据题意，所列方程正确的是（）

A、 $\frac{30}{x} - \frac{30}{1.2 x} = 20$ B、 $\frac{30}{x} - \frac{30}{x - 20} = 1.2$ C、 $\frac{30}{1.2 x} - \frac{30}{x} = 20$ D、 $\frac{30}{x - 20} - \frac{30}{x} = 1.2$

查看试题解析
12. 如图， $A D$ 是 $△ A B C$ 的中线， $E$ 是 $A D$ 上一点， $B E$ 交 $A C$ 于 $F$ ，若 $E F = A F$ ， $B E = 8$ ， $C F = 5$ ，则 $E F$ 的长度为（）

A、 $1.5$ B、 $2$ C、 $2.5$ D、 $3$

查看试题解析

二、填空题（每小题4分，共16分）

13. 若分式 $\frac{| x | - 1}{x - 1}$ 的值为0，则 $x =$ ．

查看试题解析
14. 化简： $\sqrt{18} \times \sqrt{\frac{1}{2}}$ = 。

查看试题解析
15. 把命题“同角的补角相等”改写为“如果……，那么……”的形式，如果那么．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B C = 4$ ， $△ A B C$ 的面积为 $20$ ， $A B$ 的垂直平分线 $E F$ 分别交 $A C$ ， $A B$ 边于点 $E$ ， $F$ ，若 $D$ 为 $B C$ 边的中点， $M$ 为线段 $E F$ 上一动点，则 $B M + D M$ 的最小值为．

查看试题解析

三、解答题（本大题有9题，共98分，解答应写出必要的文字说明，证明过程或演算步骤）

17. 计算：

(1)、 ${(- x^{2})}^{3} \cdot {(- 2 x^{2} y^{3})}^{2}$ ；

(2)、 $(\sqrt{6} + \sqrt{2}) (\sqrt{6} - \sqrt{2})$ ．

查看试题解析
18. 解方程或不等式组：

(1)、解分式方程 $\frac{x}{x - 2} - \frac{2}{x^{2} - 4} = 1$ ；

(2)、解不等式组 ${\begin{array}{l} 6 x + 2 > 3 x - 4 \\ \frac{2 x + 1}{3} - \frac{1 - x}{2} < 1 \end{array}$ .

查看试题解析
19. 先化简 $(\frac{x - 1}{x} - \frac{x - 2}{x + 1}) \div \frac{2 x^{2} - x}{x^{2} + 2 x + 1}$ ，然后选取一个你喜欢的x的值代入求值．

查看试题解析
20. 网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12-35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．
请根据图中的信息，回答下列问题：

(1)、这次抽样调查中共调查了人；

(2)、请补全条形统计图；并求出扇形统计图中18-23岁部分的圆心角的度数是 ▲ ；

(3)、据报道，目前我国12-35岁网瘾人数约为2000万，请估计其中12-23岁的人数；

(4)、为解决网瘾低龄化问题，保障青少年健康成长，请你提出一条合理的建议．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线 $M N$ 交 $A C$ 于点 $D$ ，交 $A B$ 于点 $E$ ． $∠ A = 40 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
22. 如图，在 $△ A B C$ 中， $B C = A C$ ， $∠ A C B = 90 °$ ，过点C作直线MN与线段AB相交， $A M ⊥ M N$ 于点M ， $B N ⊥ M N$ 于点N ．

(1)、求证： $∠ M A C = ∠ N C B$ ；

(2)、求证： $M N = A M - B N$ ．

查看试题解析
23. 某商场选购A、B两种品牌的儿童服装，A品牌服装每套进价比B品牌服装每套进价多25元，用4000元购进A种服装数量是用1500元购进B种服装数量的2倍．

(1)、求A、B两种品牌服装每套进价分别为多少元？

(2)、A品牌每套售价为130元，B品牌服装每套售价为95元，商场决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多7套，两种服装全部售出后，可使总的获利不低于7140元，则最少购进A品牌的服装多少套？

查看试题解析
24. 先观察下列的计算，再完成：
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{(\sqrt{4} - \sqrt{3})}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3} = 2 - \sqrt{3}$ ；请你直接写出下面的结果：

(1)、 $\frac{1}{\sqrt{5} + \sqrt{4}} =$ ； $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ；

(2)、根据你的猜想、归纳，运用规律计算：
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots \dots + \frac{1}{\sqrt{2023} + \sqrt{2022}}$

查看试题解析
25. 如图1，在Rt△ABC中，∠A=90°，AB=AC ，点D ， E分别在边AB ， AC上，AD=AE ，连接DC ，点M ， P ， N分别为DE ， DC ， BC的中点．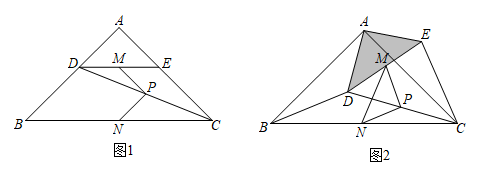

(1)、观察猜想：图1中，请判断线段PM与PN的数量关系和位置关系，并说明理由；

(2)、探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN ， BD ， CE ，判断△PMN的形状，并说明理由；

(3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=3，AB=7，请直接写出△PMN面积的最大值．

查看试题解析