贵州省黔东南苗族侗族自治州2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、单项选择题(每小题3分,共36分,每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
-
1. 下面四个美术字中可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点P关于x轴对称的点的坐标为 , 则点P的坐标为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 某种原子的直径为 , 把这个数化成小数是( )A、 B、 C、 D、5. 若分式的值为0,则x的值为( )A、 B、1 C、 D、无解6. 如图,是一副三角尺拼成的图案,则( )
2. 已知点P关于x轴对称的点的坐标为 , 则点P的坐标为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 某种原子的直径为 , 把这个数化成小数是( )A、 B、 C、 D、5. 若分式的值为0,则x的值为( )A、 B、1 C、 D、无解6. 如图,是一副三角尺拼成的图案,则( ) A、 B、 C、 D、7. 如图,是和的公共边,下列条件不能判定的是( )
A、 B、 C、 D、7. 如图,是和的公共边,下列条件不能判定的是( ) A、 , B、 , C、 , D、 ,8. 如图,已知中, , 是高, , , 则的长是( )
A、 , B、 , C、 , D、 ,8. 如图,已知中, , 是高, , , 则的长是( ) A、 B、 C、 D、9. 若是完全平方式,则的值为( )A、7或 B、 C、7或1 D、310. 在的边上找一点 , 使得 . 下面找法正确的是( )
A、 B、 C、 D、9. 若是完全平方式,则的值为( )A、7或 B、 C、7或1 D、310. 在的边上找一点 , 使得 . 下面找法正确的是( ) A、如图①以为圆心,为半径画弧,交于点 , 点为所求 B、如图②以为圆心,为半径画弧,交于点 , 点为所求 C、如图③作的垂直平分线交于点 , 点为所求 D、如图④作的垂直平分线交于点 , 点为所求11. 小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )A、 B、 C、 D、12. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,等于( )
A、如图①以为圆心,为半径画弧,交于点 , 点为所求 B、如图②以为圆心,为半径画弧,交于点 , 点为所求 C、如图③作的垂直平分线交于点 , 点为所求 D、如图④作的垂直平分线交于点 , 点为所求11. 小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )A、 B、 C、 D、12. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,等于( )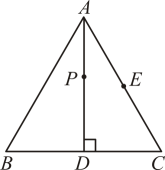 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题4分,共16分.答题请用0.5毫米黑色墨水的签字笔或钢笔直接写在答题卡的相应位置上)
-
13. 分解因式: = .14. 计算: .15. 如图,在中, , 按以下步骤作图:①以为圆心,以任意长为半径作弧,分别交 , 于点 , ;②分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 交于点若 , , 则线段的长为 .
 16. 如图,在四边形中, , 则的长为 .
16. 如图,在四边形中, , 则的长为 .
三、解答题(本题共98分)
-
17. 计算:(1)、(2)、18. 图1、图2、图3均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上,只用无刻度的直尺和圆规,在给定的网格中,分别按下列要求画图,不写作法,保留适当的作图痕迹.
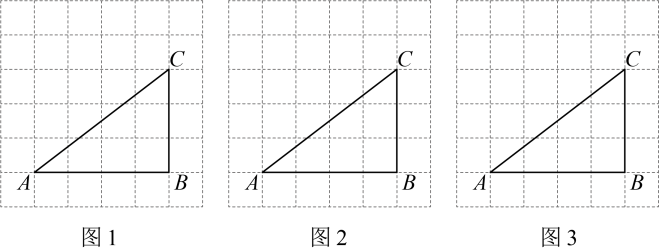 (1)、在图1中的线段上找一点 , 连接 , 使;(2)、在图2中的线段上找一点 , 连接 , 使;(3)、在图3中,作出的垂直平分线 .19. 下面某同学解分式方程的过程,请认真阅读并完成相应学习任务:
(1)、在图1中的线段上找一点 , 连接 , 使;(2)、在图2中的线段上找一点 , 连接 , 使;(3)、在图3中,作出的垂直平分线 .19. 下面某同学解分式方程的过程,请认真阅读并完成相应学习任务:解:方程两边同乘 , 得 第一步
解得 第二步
原分式方程的解为 第三步
(1)、上面的解题过程从第步开始出现错误,这一步错误的原因是;(2)、请写出正确的解题过程.20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)三个顶点的坐标分别为 . (1)、请在网格中建立平面直角坐标系;(2)、若与关于轴成轴对称,则三个顶点坐标分别为 ▲ , ▲ , ▲ ;并画出;(3)、求的面积.21. 计算:(1)、;(2)、先化简再求值: , 选择一个合适的整数代入求值.22. 阅读材料:教科书中提到“和这样的式子叫做完全平方式.”有些多项式不是完全平方式,我们可以通过添加项,凑成完全平方式,再减去这个添加项,使整个式子的值不变,这样也可以将多项式进行分解,并解决一些最值问题.例如:分解因式:
(1)、请在网格中建立平面直角坐标系;(2)、若与关于轴成轴对称,则三个顶点坐标分别为 ▲ , ▲ , ▲ ;并画出;(3)、求的面积.21. 计算:(1)、;(2)、先化简再求值: , 选择一个合适的整数代入求值.22. 阅读材料:教科书中提到“和这样的式子叫做完全平方式.”有些多项式不是完全平方式,我们可以通过添加项,凑成完全平方式,再减去这个添加项,使整个式子的值不变,这样也可以将多项式进行分解,并解决一些最值问题.例如:分解因式:求代数式的最小值
∵ , ∴当时,代数式有最小值 .
结合以上材料解决下面的问题:
(1)、分解因式:;(2)、求代数式的最小值;(3)、当为何值时,有最小值?最小值是多少?23. 如图,点C在线段上, , , , 于点F . (1)、求证:;(2)、若 , 求的度数;(3)、求证:平分 .24. 为支援灾区,某学校献爱心活动小组准备用筹集的资金购买甲、乙两种型号的学习用品共1000件.已知乙型学习用品的单价比甲型学习用品的单价多20元,用180元购买乙型学习用品与用120元购买甲型学习用品的件数相同.(1)、求甲,乙两种学习用品的单价各是多少元;(2)、若购买这批学习用品的费用不超过48000元,则最多购买乙型学习用品多少件?25. 已知,在等边三角形中,点E在上,点D在的延长线上,且 .
(1)、求证:;(2)、若 , 求的度数;(3)、求证:平分 .24. 为支援灾区,某学校献爱心活动小组准备用筹集的资金购买甲、乙两种型号的学习用品共1000件.已知乙型学习用品的单价比甲型学习用品的单价多20元,用180元购买乙型学习用品与用120元购买甲型学习用品的件数相同.(1)、求甲,乙两种学习用品的单价各是多少元;(2)、若购买这批学习用品的费用不超过48000元,则最多购买乙型学习用品多少件?25. 已知,在等边三角形中,点E在上,点D在的延长线上,且 . (1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).
(1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).