贵州省铜仁市碧江区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、选择题:(每小题3分,共36分.在每小题给出的四个选项中,只有一正确选项,请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满.)
-
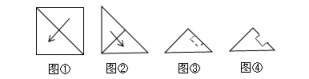
1. 数1,0, , 中最大的是( )A、0 B、1 C、 D、2. 近年来中国取得的科技成就有:北斗全球卫星导航系统平均精度2~3米;中国高铁运营里程超米;“奋斗者”号载人潜水器最深下潜至10909米;中国嫦娥五号带回月壤重量1731克等.其中数据用科学记数法表示为( )A、 B、 C、 D、3. 将一张正方形纸片按图①、图②所示的方式依次对折后,再沿图③中的虚线剪裁,最后将图④中的纸片打开铺平,所得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 单项式 的系数和次数分别是( )A、 ,6 B、 ,5 C、 ,5 D、 ,55. 下列调查中,适合用普查的是( )A、中央电视台春节联欢晚会的收视率 B、一批灯泡的寿命 C、全国中学生的节水意识 D、某班每一位同学的体育达标情况6. 已知等式a=b , 则下列变形错误的是( )A、|a|=|b| B、a+b=0 C、a2=b2 D、2a﹣2b=07. 下列各组代数式中,不是同类项的是( )A、和 B、和 C、和3 D、和8. 已知x=-3是方程2x+3m=3的解,则m的值为( )A、3 B、1 C、-1 D、-39. 下列说法正确的个数是( )
4. 单项式 的系数和次数分别是( )A、 ,6 B、 ,5 C、 ,5 D、 ,55. 下列调查中,适合用普查的是( )A、中央电视台春节联欢晚会的收视率 B、一批灯泡的寿命 C、全国中学生的节水意识 D、某班每一位同学的体育达标情况6. 已知等式a=b , 则下列变形错误的是( )A、|a|=|b| B、a+b=0 C、a2=b2 D、2a﹣2b=07. 下列各组代数式中,不是同类项的是( )A、和 B、和 C、和3 D、和8. 已知x=-3是方程2x+3m=3的解,则m的值为( )A、3 B、1 C、-1 D、-39. 下列说法正确的个数是( )①两点确定一条直线;
②两条直线相交只有一个交点;
③两点之间线段最短;
④将一条线段分成相等线段的点叫做线段的中点.
A、1 B、2 C、3 D、410. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:
乙:
丙:
丁:
其中正确的是( )
 A、甲乙 B、丙丁 C、甲丙 D、乙丁11. 为了帮助学生减轻压力,学会自我放松,某学校计划组织九年级学生开展一次“远足行动”,去时步行,返回时坐车.小明发现:“若租用35座的客车要若干辆,且有3人没有座位座;若租用40座的客车,则可以少租1辆,且有一辆空2个座位.”若设租用35座的客车x辆,则可列方程( )A、35x+3=40(x-1)+2 B、35x+3=40(x-1)-2 C、35x-3=40(x-1)+2 D、35x-3=40(x-1)-212. 数学探究小组在一次探究课上,小明突然发现有这样一个有趣的数学规律,已知一组数列: , , , …,当时,则等于( )A、3 B、 C、 D、
A、甲乙 B、丙丁 C、甲丙 D、乙丁11. 为了帮助学生减轻压力,学会自我放松,某学校计划组织九年级学生开展一次“远足行动”,去时步行,返回时坐车.小明发现:“若租用35座的客车要若干辆,且有3人没有座位座;若租用40座的客车,则可以少租1辆,且有一辆空2个座位.”若设租用35座的客车x辆,则可列方程( )A、35x+3=40(x-1)+2 B、35x+3=40(x-1)-2 C、35x-3=40(x-1)+2 D、35x-3=40(x-1)-212. 数学探究小组在一次探究课上,小明突然发现有这样一个有趣的数学规律,已知一组数列: , , , …,当时,则等于( )A、3 B、 C、 D、二、填空题:(每小题4分,共16分)
-
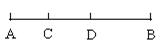
13. 如图,已知点C是线段AD的中点,AB=20cm,BD=8cm,则BC=cm.
 14. 计算: .15. 元旦期间,“茂业”商场对某品牌羽绒服实行七折销售,张阿姨到该商场购买了一件该品牌的羽绒服发现比不打折时可省下240元,那么该品牌的标价是元.16. 如图是用小圆摆成的图案,按照这样的规律摆下去,第⑦个图案需要的小圆个数为个小圆,第n个图形为小圆.
14. 计算: .15. 元旦期间,“茂业”商场对某品牌羽绒服实行七折销售,张阿姨到该商场购买了一件该品牌的羽绒服发现比不打折时可省下240元,那么该品牌的标价是元.16. 如图是用小圆摆成的图案,按照这样的规律摆下去,第⑦个图案需要的小圆个数为个小圆,第n个图形为小圆.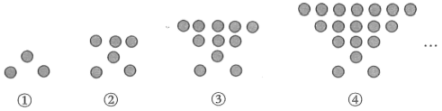
三、计算题:(共98分)(第17、18各12分,19、20题8分,第21、22题10分,23、24题12分,25题14分)
-
17. 计算:(1)、(2)、若代数式的值是6,求代数式的值.18. 解方程:(1)、;(2)、 .19. 若a , b互为相反数,c , d互为倒数,m的绝对值为4,求的值.20. 观察有理数a , b , c在数轴上的位置,如图所示,
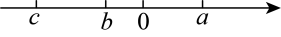 (1)、比较大小: 0, 0,0;(2)、化简: .21. 如图,C为线段上一点,D在线段上,且 , E为的中点.
(1)、比较大小: 0, 0,0;(2)、化简: .21. 如图,C为线段上一点,D在线段上,且 , E为的中点. (1)、若 , , 求线段、的长;(2)、试说明: .22. 老师在黑板上写了一个正确的演算过程,随后用手掌捂住了多项式形式如下:
(1)、若 , , 求线段、的长;(2)、试说明: .22. 老师在黑板上写了一个正确的演算过程,随后用手掌捂住了多项式形式如下: (1)、求所捂的多项式;(2)、若a,b满足: , 请求出所捂的多项式的值.23. 联合国规定每年的6月5日是“世界环境日”.碧江区某中学成立了“环保小卫士”研学小组对周边小区部分居民开展了以“垃圾分类,爱护环境”为主题的问卷调查,调查内容如下:
(1)、求所捂的多项式;(2)、若a,b满足: , 请求出所捂的多项式的值.23. 联合国规定每年的6月5日是“世界环境日”.碧江区某中学成立了“环保小卫士”研学小组对周边小区部分居民开展了以“垃圾分类,爱护环境”为主题的问卷调查,调查内容如下:A:能将垃圾放到规定地点,并会考虑垃圾分类
B:能将垃圾放到规定地点,但不会考虑垃圾分类
C:基本能将垃圾放到规定地点,偶尔会乱扔垃圾
研学小组将调查结果制成下面两幅不完整的统计图:
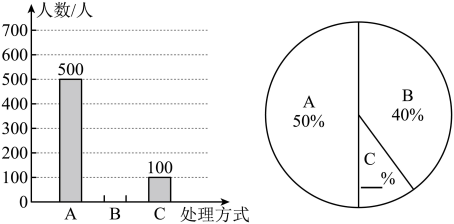 (1)、研学小组一共调查了人,扇形统计图中C部分的圆心角度;(2)、将上面的条形统计图和扇形统计图补充完整;(3)、如果你是“环保小卫士”成员,请根据以上调查结果谈谈你的想法和建议.24. 铜仁南方电网为响应国家节能减排政策,对铜仁居民用户实行阶梯电价收费,月用电量210度之内(包括210度),每度价格元,用电量210度至350度,每度比第一档次提价元,月用电量350度以上,每度比第一档提价元.
(1)、研学小组一共调查了人,扇形统计图中C部分的圆心角度;(2)、将上面的条形统计图和扇形统计图补充完整;(3)、如果你是“环保小卫士”成员,请根据以上调查结果谈谈你的想法和建议.24. 铜仁南方电网为响应国家节能减排政策,对铜仁居民用户实行阶梯电价收费,月用电量210度之内(包括210度),每度价格元,用电量210度至350度,每度比第一档次提价元,月用电量350度以上,每度比第一档提价元.例:若某户月用电量400度,则需交电费 . 如果按此方案计算,小华家5月份的电费为元.
问题:
(1)、则小华家该月用电量属于第几档?并通过计算得出用电量是多少?(2)、若小红家这个月用电a度,交电费为b元,请你用含字母a , b表示小红家的用电费用.25. 以直线上一点O为端点,在直线的上方作射线 , 使 , 将一个直角三角板的直角顶点放在O处,即 , 直角三角板可绕顶点O转动,在转动的过程中,直角三角板所有部分始终保持在直线上或上方.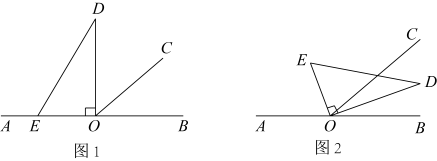 (1)、如图1,若直角三角板的一边在射线上,则;(2)、将直角三角板绕点O转动后,使其一边在的内部,如图2所示,
(1)、如图1,若直角三角板的一边在射线上,则;(2)、将直角三角板绕点O转动后,使其一边在的内部,如图2所示,①若恰好平分 , 求此时的度数;
②若 , 求此时的度数;
(3)、直角三角板在绕点O转动的过程中,与之间存在一定的数量关系,请直接写出来,不必说明理由.