贵州省贵阳市南明区2023-2024学年八年级上学期期末数学试卷
试卷更新日期:2024-02-20 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列各数是无理数的是( )A、 B、 C、 D、2. 贵阳甲秀楼始建于明朝万历年间,是贵阳的地标式建筑,位于贵阳市南明区翠微巷的南明河上,若小明将位于翠微巷的翠微园入口的位置记为原点,建立如图所示的平面直角坐标系,则下列哪个坐标可以表示甲秀楼的位置( )
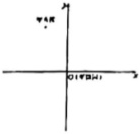 A、 B、 C、 D、3. 下列命题中,属于假命题的是( )A、对顶角相等 B、正比例函数是一次函数 C、内错角相等 D、三角形的三个内角和等于4. 下列各组数中,是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,5. 一次函数的大致图象是( )A、
A、 B、 C、 D、3. 下列命题中,属于假命题的是( )A、对顶角相等 B、正比例函数是一次函数 C、内错角相等 D、三角形的三个内角和等于4. 下列各组数中,是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,5. 一次函数的大致图象是( )A、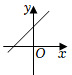 B、
B、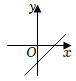 C、
C、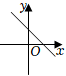 D、
D、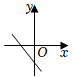 6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、 C、 D、7. 在年贵州某大学数学与统计学院的研究生入学考试中,三名考生甲、乙、丙在笔试、面试中的成绩百分制如下表所示,你觉得被录取的考生是( )
6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、 C、 D、7. 在年贵州某大学数学与统计学院的研究生入学考试中,三名考生甲、乙、丙在笔试、面试中的成绩百分制如下表所示,你觉得被录取的考生是( )考生
笔试
面试
甲
乙
丙
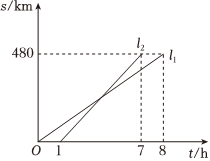
A、甲 B、乙 C、丙 D、无法判断8. 如图,已知一次函数和的图象相交于点 , 则根据图象可得二元一次方程组的解是( )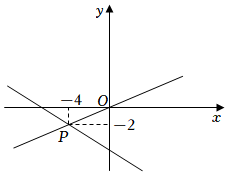 A、 B、 C、 D、9. 如图,一个长方体形盒子的长、宽、高分别为厘米、厘米、厘米,在长方体一底面的顶点有一只蚂蚁,它想吃点处的食物,沿长方体侧面爬行的最短路程是( )
A、 B、 C、 D、9. 如图,一个长方体形盒子的长、宽、高分别为厘米、厘米、厘米,在长方体一底面的顶点有一只蚂蚁,它想吃点处的食物,沿长方体侧面爬行的最短路程是( ) A、厘米 B、厘米 C、厘米 D、厘米10. 在平面直角坐标系中,若干个边长为个单位长度的等边三角形,按如图中的规律摆放点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“”的路线运动,设第秒点运动到点为正整数 , 则点的坐标是( )
A、厘米 B、厘米 C、厘米 D、厘米10. 在平面直角坐标系中,若干个边长为个单位长度的等边三角形,按如图中的规律摆放点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“”的路线运动,设第秒点运动到点为正整数 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共4小题,每小题4分,共16分。
-
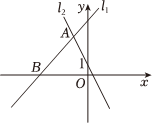
11. 64的算术平方根是.12. 已知中,三个内角的度数比为:::: , 则中最大的内角度数是 .13. 若 , 则 .14. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .
三、解答题:本题共7小题,共54分。解答应写出文字说明,证明过程或演算步骤。
-
15.(1)、计算:;(2)、下面是小华同学解二元一次方程组的过程,请仔细观察回答下面问题.
解: , 得
, 得
将代入 , 得
所以原方程组的解是
1 以上过程有两处关键性错误,第一次出错在 ▲ 步填序号 , 第二次出错在 ▲ 步填序号;
2 请你帮小华同学写出正确的解题过程.
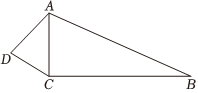
16. 如图,已知点、分别在射线和上, , 求证: .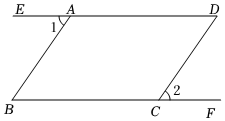 17. 在平面直角坐标系中的位置如图所示,点的坐标是 .
17. 在平面直角坐标系中的位置如图所示,点的坐标是 . (1)、点的坐标为 , , 点的坐标为 , ;(2)、画出关于轴对称的图形;(3)、求的面积.18. 南明区某学校七、八年级举行“一二九”演讲比赛,根据初赛成绩各选出了名选手编号分别为、、、、组成七年级代表队、八年级代表队参加学校决赛,根据这名选手的决赛成绩满分为分 , 制作了如下的统计图表:
(1)、点的坐标为 , , 点的坐标为 , ;(2)、画出关于轴对称的图形;(3)、求的面积.18. 南明区某学校七、八年级举行“一二九”演讲比赛,根据初赛成绩各选出了名选手编号分别为、、、、组成七年级代表队、八年级代表队参加学校决赛,根据这名选手的决赛成绩满分为分 , 制作了如下的统计图表:二
平均数
中位数
众数
方差
七年级
八年级
 (1)、表格中 ;(2)、请求出八年级代表队参加学校决赛的平均成绩;(3)、要从这两个年级代表队中选出一个年级,代表学校去参加南明区的比赛,你认为应该选择哪个年级代表队?请说明理由.19. 某城市响应国家绿色环保理念,提倡在全市范围内低碳出行,因此新能源汽车逐渐成为人们喜爱的交通工具某汽车销售公司计划年购进一批新能源汽车,据了解,辆型汽车、辆型汽车的进价共计万元;辆型汽车、辆型汽车的进价共计万元,型、型汽车每辆进价分别为多少万元?
(1)、表格中 ;(2)、请求出八年级代表队参加学校决赛的平均成绩;(3)、要从这两个年级代表队中选出一个年级,代表学校去参加南明区的比赛,你认为应该选择哪个年级代表队?请说明理由.19. 某城市响应国家绿色环保理念,提倡在全市范围内低碳出行,因此新能源汽车逐渐成为人们喜爱的交通工具某汽车销售公司计划年购进一批新能源汽车,据了解,辆型汽车、辆型汽车的进价共计万元;辆型汽车、辆型汽车的进价共计万元,型、型汽车每辆进价分别为多少万元?