湖南省长沙市雨花区2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

1. 计算 $| - 2024 |$ 的结果是（）

A、 $2024$ B、 $\frac{1}{2024}$ C、 $- 2024$ D、 $- \frac{1}{2024}$

查看试题解析
2. 2023年 $1 - 10$ 月，我国企业在“一带一路”共建国家非金融类直接投资 $1816.9$ 亿元人民币，同比增长 $27 %$ ．数字 $1816.9$ 亿用科学记数法表示为（　）

A、 $1.8169 \times 1 0^{11}$ B、 $1.8169 \times 1 0^{8}$ C、 $1.8169 \times 1 0^{12}$ D、 $1816.9 \times 1 0^{8}$

查看试题解析
3. 单项式 $- 2023 m n^{2}$ 的系数是（　）

A、2023 B、 $- 2023$ C、2 D、3

查看试题解析
4. 若一个角为 $45 °$ ，则其补角的度数为（　　）

A、 $55 °$ B、 $45 °$ C、 $155 °$ D、 $135 °$

查看试题解析
5. 下列计算中，正确的是（）

A、 $a + a^{2} = a^{3}$ B、 $2 a + 3 b = 5 a b$ C、 $2 a + 3 a = 6 a$ D、 $a + 2 a = 3 a$

查看试题解析
6. 如图是一个立体图形的展开图，则该立体图形是（　　）

A、长方体 B、三棱锥 C、圆柱 D、圆锥

查看试题解析
7. 如图， $∠ D O B = 2 ∠ A O B$ ， $O C$ 平分 $∠ A O D$ ， $∠ B O C = 18 °$ ，则 $∠ A O D$ 度数为（　　）

A、 $98 °$ B、 $108 °$ C、 $110 °$ D、 $120 °$

查看试题解析
8. 若代数式 $x - 3 y$ 的值为2，则 $5 - 2 x + 6 y$ 的值为（）

A、1 B、 $- 2$ C、9 D、 $- 7$

查看试题解析
9. 如图，在两个完全相同的大长方形中各放入五个完全一样的白色小长方形，得到图（1）与图（2）．若 $A B = m$ ，则图（1）与图（2）阴影部分周长的差是（）

A、 $m$ B、 $\frac{5}{4} m$ C、 $\frac{6}{5} m$ D、 $\frac{7}{6} m$

查看试题解析
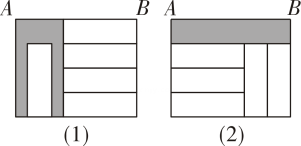10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格，将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，如图是一个未完成的幻方，则 $x$ 的值为（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. $\sqrt{5}$ 的相反数是．

查看试题解析
12. 若 $x = - 2$ 是关于 $x$ 的方程 $2 x + m - 4 = 0$ 的解，则 $m$ 的值为

查看试题解析
13. 若5a^m⁺²b⁴与﹣a⁵bⁿ的和仍是一个单项式，则m+n＝．

查看试题解析
14. 如图，已知线段AB=8cm，点M是AB的中点，P是线段MB上一点，N为PB的中点，NB=1.5cm，则线段MP =cm．

查看试题解析
15. 由于换季，商场准备对某商品打折出售，如果按原售价的七五折出售，将亏损25元，而按原售价的九折出售，将盈利20元，则该商品的原售价为元．

查看试题解析
16. 某电视台组织知识竞赛，共设20道选择题，各题分值相同，每题必答，下表记录了其中5位参赛者的得分情况，参赛者 $F$ 说自己得分是71至80之间的一个整数，请根据图表信息推断参赛者 $F$ 的得分为．
参赛者
答对题数
答错题数
得分
A
20
0
100
B
19
1
94
C
18
2
88
D
14
6
64
E
10
10
40

查看试题解析

三、解答题（本大题共9小题，满分72分）

17. 计算： $- 2^{2} - 12 \times (\frac{1}{2} - \frac{1}{3})$ ．

查看试题解析
18. 解方程： $\frac{2 x + 1}{3} = \frac{5 x - 1}{6}$ ．

查看试题解析
19. 若有理数a ， b ， c在数轴上的位置如图所示，其中O是原点，且 $| b | = | c |$ ．

(1)、用“＜”号把 $a ， b ， - a ， - b$ 连接起来；

(2)、 $b + c$ 的值是多少？

(3)、判断 $a + b$ 与 $a + c$ 的符号．

查看试题解析
20. 某商场从厂家购进100个整理箱，按进价的1.5倍进行标价．当按标价卖出80个整理箱后，恰逢元旦，剩余的部分以标价的九折出售完毕，所得利润共1880元，求每个整理箱的进价．

查看试题解析
21. 整体代换是数学的一种思想方法，例如：已知 $x^{2} + x = 0$ ，求 $x^{2} + x + 1186$ 的值，我们将 $x^{2} + x$ 作为一个整体代入，则原式 $= 0 + 1186 = 1186$ ．仿照上面的解题方法，完成下面的问题：

(1)、如果 $a + b = 6$ ，求 $2 (a + b) - 4 a - 4 b + 2$ 的值；

(2)、若 $a^{2} + 2 a b = 20 ， b^{2} + 2 a b = 8$ ，求 $2 a^{2} - 4 b^{2} - 4 a b$ 的值．

查看试题解析
22. 数学课上，张老师出示了这样一道题：“求多项式 $7 a^{3} + 3 a^{2} b + 3 a^{3} + 6 a^{3} b - 3 a^{2} b - 10 a^{3} - 6 a^{3} b - 1$ 的值，其中 $a = 2024 ， b = - 2$ ． ”小雅同学思索片刻后指出：“ $a = 2024 ， b = - 2$ 是多余的条件”．师生讨论后，一致认为小雅说法是正确的．

(1)、请你说明正确的理由；

(2)、受此启发，老师又出示了一道题目：“无论x ， y取任何值，多项式 $2 x^{2} + a x - 5 y + b - 2 (b x^{2} - \frac{3}{2} x - \frac{5}{2} y - 3)$ 值都不变，求a ， b的值”．请你解决这个问题．

查看试题解析
23. 如图1，点C在线段 $A B$ 上，图中共有三条线段 $A B ， A C$ 和 $B C$ ，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段 $A B$ 的“巧点”．

(1)、若点C是线段 $A B$ 的中点，判断C是否是线段 $A B$ 的“巧点”；

(2)、如图2，已知 $A B = 15 c m$ ，动点P从点A出发，以2cm/s的速度沿AB向点B匀速运动；点Q从点B出发，以1cm/s的速度沿 $B A$ 向点A匀速运动，点P ， Q同时出发，设移动的时间为t（s），当其中一点到达终点时，运动停止．
①当t为何值时，P、Q重合？
②当t为何值时，Q为 $A P$ 的“巧点”？

查看试题解析
24. 某公园有以下A ， B ， C三种购票方式：
种类
购票方式
A
一次性使用门票，每张12元
B
年票每张120元，持票者每次进入公园无需再购买门票
C
年票每张60元，持票者进入公园时需再购买每次6元的门票

(1)、某游客一年中进入该公园共有 $a$ 次，分别求三种购票方式一年的费用；（用含 $a$ 的代数式表示）

(2)、某游客一年中进入该公园共有12次，选择哪种购买方式比较优惠？请通过计算说明．

(3)、已知甲，乙，丙三人分别按A ， B ， C三种方式购票，且他们一年中进入该公园的次数相同．一年中，若甲所花的费用比乙和丙两人所花费用之和的一半还多36元，求甲一年中进入该公园的次数．

查看试题解析
25. 一块三角板按如图1方式摆放，其中边 $O A$ 与直线 $E F$ 重合， $∠ A O B = 30 °$ ，射线 $O C$ 在直线 $E F$ 上方，且 $∠ E O C = 50 °$ ，作 $∠ B O C$ 的角平分线 $O D$ ．

(1)、求图1中 $∠ C O D$ 的度数．

(2)、如图2，将三角板 $A O B$ 绕点 $O$ 按逆时针方向旋转一个角度 $α$ ，在转动过程中三角板一直处于直线 $E F$ 的上方．
①当 $∠ C O D = 20 °$ 时，求旋转角 $α$ 的值；
②在转动过程中是否存在 $∠ B O E = 3 ∠ A O C$ ？若存在，求此时 $α$ 的值；若不存在，请说明理由．

查看试题解析

参赛者	答对题数	答错题数	得分
A	20	0	100
B	19	1	94
C	18	2	88
D	14	6	64
E	10	10	40

种类	购票方式
A	一次性使用门票，每张12元
B	年票每张120元，持票者每次进入公园无需再购买门票
C	年票每张60元，持票者进入公园时需再购买每次6元的门票