湖南省长沙市雨花区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

1. 计算 $- \sqrt{\frac{1}{4}}$ 的结果为（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-2 D、2

查看试题解析
2. 下列等式从左到右的变形一定正确的是（）

A、 $\frac{b}{a} = \frac{b + 1}{a + 1}$ B、 $\frac{a b}{a^{2}} = \frac{b}{a}$ C、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ D、 $\frac{- b}{- a} = - \frac{b}{a}$

查看试题解析
3. 随着自主研发能力的增强，上海微电子发布消息称已经成功研发出了 $0.000000028 m$ 工艺的国产沉浸式光刻机，数据 $0.000000028$ 用科学记数法表示为（）

A、 $0.28 \times 1 0^{- 9}$ B、 $2.8 \times 1 0^{- 8}$ C、 $28 \times 1 0^{- 8}$ D、 $2.8 \times 1 0^{- 7}$

查看试题解析
4. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt[3]{(- x)^{3}} = - x$ D、 $\sqrt{(- x)^{2}} = - x$

查看试题解析
5. 已知： $(2 x + 1) (x - 3) = 2 x^{2} + px + q$ ，则p，q的值分别为（）

A、5，3 B、5，−3 C、−5，3 D、−5， −3

查看试题解析
6. 若关于x的方程 $\frac{m}{x + 1} - \frac{2}{x + 1} = 1$ 的解为负数，则m的取值范围是（）

A、 $m < 2$ B、 $m < 3$ C、 $m < 2$ 且 $3 m \neq 1$ D、 $m < 3$ 且 $m \neq 2$

查看试题解析
7. 如图所示，BC ， AE是锐角 $△ A B F$ 的高，相交于点D ，若 $A D = B F$ ， $A F = 7$ ， $C F = 2$ ，则BD的长为（）．

A、2 B、3 C、4 D、5

查看试题解析
8. 如图， $B D = B C$ ， $B E = C A$ ， $∠ D B E = ∠ C = 62 °$ ， $∠ B D E = 75 °$ ，则 $∠ A F D$ 的度数等于（）

A、 $30 °$ B、 $32 °$ C、 $33 °$ D、 $35 °$

查看试题解析
9. 一条船往返于甲，乙两港之间，由甲至乙是顺水行驶，由乙至甲是逆水行驶，已知船在静水中的速度为 $8 k m / h$ ，平时逆水航行与顺水航行所用的时间比为 $2 ： 1$ ，某天恰逢暴雨，水流速度是原来的2倍，这条船往返共用了 $9 h$ ．则甲，乙两港之间的距离为（）

A、 $\frac{160 k m}{3}$ B、 $15 k m$ C、 $\frac{25}{2} k m$ D、 $20 k m$

查看试题解析
10. 如图，C为线段AE上一动点（不与点A ， E重合），在AE同侧分别作等边△ABC和等边△ECD ， AD与BE交于点O ， AD与BC交于点P ， BE与CD交于点Q连接PQ ．以下五个结论正确的是（）
① $A D = B E$ ；②PQ∥AE； ③ $A P = B Q$ ；④ $D E = D P$ ；⑤ $∠ A O B = 6 0^{∘}$

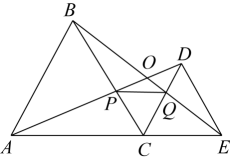A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. 分解因式：mn²+6mn+9m= ．

查看试题解析
12. 已知 $△ A B C ≌ △ D E F$ ， $B C = E F = 10 c m$ ，若 $△ D E F$ 的面积是 $40 c m^{2}$ ，则 $△ A B C$ 中 $B C$ 边上的高是 $c m$ .

查看试题解析
13. 二次根式 $\sqrt{50 a}$ 是一个整数，那么正整数a的最小值是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C = 8 ， B C = 5$ ， $A B$ 的垂直平分线交 $A C$ 于D ，交 $A B$ 于E ，则 $△ B C D$ 的周长为．

查看试题解析
15. 如图， $∠ 1$ 是五边形的一个外角．若 $∠ 1 = 70 °$ ，则 $∠ A + ∠ B + ∠ C + ∠ D$ 的度数为．

查看试题解析
16. 已知 $\frac{1}{x} - \frac{1}{y} = 3$ ，则代数式 $\frac{3 x - 21 x y - 3 y}{x - 2 x y - y}$ 的值为．

查看试题解析

三、解答题（本大题共9小题，满分72分）

17. 计算： ${(- 3 a^{2} b)}^{2} \cdot {(- a^{2} c^{3})}^{3}$ ．

查看试题解析
18. 解方程： $\frac{x}{x - 3} - \frac{1}{x + 3} = 1$ ．

查看试题解析
19. 在直角坐标系中，有点A（3，0），B（0，4），若有一个直角三角形与Rt△ABO全等且它们只有一条公共直角边，请写出这些直角三角形各顶点的坐标（不要求写计算过程）．（至少写出三个）

查看试题解析
20. 先化简，再求值： $(1 - \frac{2}{x - 1}) \cdot \frac{x^{2} - x}{x^{2} - 6 x + 9}$ ，其中 $x = 13$ ．

查看试题解析
21. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.

(1)、求∠F的度数；

(2)、若CD=2，求DF的长.

查看试题解析
22. 观察下面的因式分解过程：
am+an+bm+bn＝（am+an）+（bm+bn）＝a（m+n）+b（m+n）＝（m+n）（a+b）
利用这种方法解决下列问题：

(1)、因式分解：2a+6b﹣3am﹣9bm

(2)、△ABC三边a，b，c满足a²﹣ac﹣ab+bc＝0，判断△ABC的形状．

查看试题解析
23. 某中学为了创设“书香校园”，准备购买 $A, B$ 两种书架，用于放置图书.在购买时发现， $A$ 种书架的单价比 $B$ 种书架的单价多20元，用600元购买 $A$ 种书架的个数与用480元购买 $B$ 种书架的个数相同.

(1)、求 $A, B$ 两种书架的单价各是多少元？

(2)、学校准备购买 $A, B$ 两种书架共15个，且购买的总费用不超过1400元，求最多可以购买多少个 $A$ 种书架？

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C = 2$ ， $∠ B = 36 °$ ，点D在线段 $B C$ 上运动（点D不与点B、C重合），连接 $A D$ ，作 $∠ A D E = 36 °$ ， $D E$ 交线段 $A C$ 于点E ．

(1)、当 $∠ B D A = 128 °$ 时， $∠ E D C =$ ， $∠ A E D =$ ；

(2)、线段 $D C$ 的长度为何值时， $△ A B D ≌ △ D C E$ ？请说明理由；

(3)、在点D的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，请直接写出 $∠ B D A$ 的度数；若不可以，请说明理由．

查看试题解析
25. 阅读下述材料：
我们在学习二次根式时，熟悉的分母有理化以及应用．其实，有一个类似的方法叫做“分子有理化”，
与分母有理化类似，分母和分子都乘以分子的有理化因式，从而消掉分子中的根式，比如： $\sqrt{7} - \sqrt{6} = \frac{(\sqrt{7} - \sqrt{6}) (\sqrt{7} + \sqrt{6})}{\sqrt{7} + \sqrt{6}} = \frac{1}{\sqrt{7} + \sqrt{6}}$ ，
分子有理化可以用来比较某些二次根式的大小，也可以用来处理一些二次根式的最值问题．例如：
比较 $\sqrt{7} - \sqrt{6}$ 和 $\sqrt{6} - \sqrt{5}$ 的大小．可以先将它们分子有理化如下： $\sqrt{7} - \sqrt{6} = \frac{1}{\sqrt{7} + \sqrt{6}}$ ， $\sqrt{6} - \sqrt{5} = \frac{1}{\sqrt{6} + \sqrt{5}}$ ，
因为 $\sqrt{7} + \sqrt{6} > \sqrt{6} + \sqrt{5}$ ，所以 $\sqrt{7} - \sqrt{6} < \sqrt{6} - \sqrt{5}$ ．
再例如：求 $y = \sqrt{x + 2} - \sqrt{x - 2}$ 的最大值．做法如下：
解：由 $x + 2 \geq 0 ， x - 2 \geq 0$ 可知 $x \geq 2$ ，而 $y = \sqrt{x + 2} - \sqrt{x - 2} = \frac{4}{\sqrt{x + 2} + \sqrt{x - 2}}$ ，
当 $x = 2$ 时，分母 $\sqrt{x + 2} + \sqrt{x - 2}$ 有最小值2，所以y的最大值是2．
解决下述问题：

(1)、比较 $3 \sqrt{2} - 4$ 和 $2 \sqrt{3} - \sqrt{10}$ 的大小；

(2)、求 $y = \sqrt{1 - x} + \sqrt{1 + x} - \sqrt{x}$ 的最大值和最小值．

查看试题解析