湖南省株洲市渌口区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、选择题(本题共10小题,每小题3分,满分30分)
-
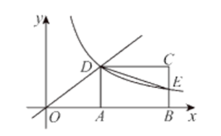
1. 若x2=9,则x=( )A、3 B、-3 C、±3 D、812. 反比例函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限3. 抛物线的顶点坐标是( )A、(﹣2,﹣3) B、(﹣2,3) C、(2,﹣3) D、(2,3)4. 小颖随机抽查她家6月份某5天的日用电量(单位:度),结果如下:9,11,7,10,8.根据这些数据,估计她家6月份的用电量为( )A、180度 B、210度 C、240度 D、270度5. 关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、6. 某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为( )A、5 B、6 C、7 D、87. 如图,已知 , , 若的长度为6,则的长度为( )
 A、4 B、9 C、12 D、8. 如图,某游乐场一个跷跷板支撑柱垂直地面, , 当的一端A着地时, , 若 , 则( )
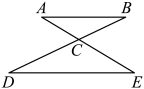
A、4 B、9 C、12 D、8. 如图,某游乐场一个跷跷板支撑柱垂直地面, , 当的一端A着地时, , 若 , 则( )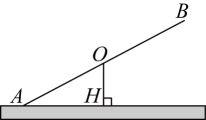 A、 B、 C、 D、9. 刘老师从全校2000名学生每天体育锻炼时长的问卷中,随机抽取部分学生的答卷,并将结果统计后绘制成如图所示的条形统计图,其中一部分被墨迹遮盖.已知每天锻炼时长为1小时的学生人数占样本总人数的 , 则下列说法正确的是( )
A、 B、 C、 D、9. 刘老师从全校2000名学生每天体育锻炼时长的问卷中,随机抽取部分学生的答卷,并将结果统计后绘制成如图所示的条形统计图,其中一部分被墨迹遮盖.已知每天锻炼时长为1小时的学生人数占样本总人数的 , 则下列说法正确的是( )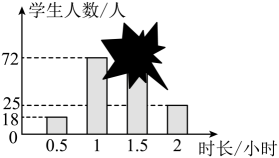 A、抽取的学生人数小于 B、名学生是样本 C、被调查学生中,锻炼时长为1.5小时的人数最多 D、该校锻炼时长为2小时的学生约有名10. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )
A、抽取的学生人数小于 B、名学生是样本 C、被调查学生中,锻炼时长为1.5小时的人数最多 D、该校锻炼时长为2小时的学生约有名10. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )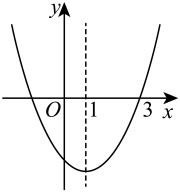 A、 B、 C、 D、点在函数图象上
A、 B、 C、 D、点在函数图象上二、填空题(共6个小题,每小题3分,满分18分)
-
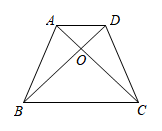
11. 计算: .12. 设方程的两根分别是 , , 则的值为 .13. 在中, , 已知 , 那么的值是 .14. 已知二次函数的图象与轴的一个交点为 , 则它与轴的另一个交点的坐标是 .15. 如图所示,已知在梯形ABCD中, , , 则 .
 16. 如图,已知 , , 把绕原点逆时针旋转得到 , 点的对应点为点 , 若反比例函数的图象经过点 , 则的值是 .
16. 如图,已知 , , 把绕原点逆时针旋转得到 , 点的对应点为点 , 若反比例函数的图象经过点 , 则的值是 .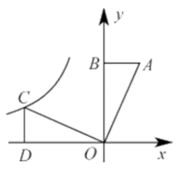
三、解答题(共9个小题,满分72分,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,要有必需的解题步骤与过程)
-
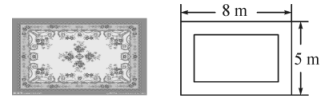
17. 计算:18. 一块四周镶有宽度相等的花边的地毛如图,它的长为 , 宽为 , 如果地毛炎中央长方形图案的面积为 , 问花边有多宽?
 19. 江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树的点处,然后观测者沿着直线后退到点 , 这时恰好在镜子里看到树梢顶点 , 再用皮尺量得 , 观测者目高 , 则树高约是多少?
19. 江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树的点处,然后观测者沿着直线后退到点 , 这时恰好在镜子里看到树梢顶点 , 再用皮尺量得 , 观测者目高 , 则树高约是多少? 20. 已知(且).(1)、化简A;(2)、若点在反比例函数的图象上,求A的值.21. 如图,点在轴的正半轴上,抛物线与直线在第一象限内的交点为 , 试求的值.
20. 已知(且).(1)、化简A;(2)、若点在反比例函数的图象上,求A的值.21. 如图,点在轴的正半轴上,抛物线与直线在第一象限内的交点为 , 试求的值. 22. 某学校为了了解学生每天零花钱的情况,从该校学生中随机抽取部分学生对每天零花钱情况进行了问卷调查和统计,并绘制成如图所示的两个统计图.请你根据以上信息回答下列问题:
22. 某学校为了了解学生每天零花钱的情况,从该校学生中随机抽取部分学生对每天零花钱情况进行了问卷调查和统计,并绘制成如图所示的两个统计图.请你根据以上信息回答下列问题: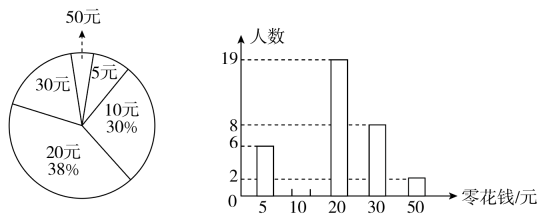 (1)、在这次调查中,共抽取的学生有多少人?(2)、在这次调查中,每天零花钱为元的学生有多少人?并补全条形统计图.(3)、该校共有学生人,请你估计这个学校学生每天零花钱的总数.23. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)(参考数据: , , , )
(1)、在这次调查中,共抽取的学生有多少人?(2)、在这次调查中,每天零花钱为元的学生有多少人?并补全条形统计图.(3)、该校共有学生人,请你估计这个学校学生每天零花钱的总数.23. 贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚为起点,沿途修建、两段长度相等的观光索道,最终到达山顶处,中途设计了一段与平行的观光平台为 . 索道与的夹角为 , 与水平线夹角为 , 两处的水平距离为 , , 垂足为点 . (图中所有点都在同一平面内,点在同一水平线上)(参考数据: , , , )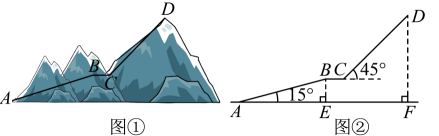 (1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).
(1)、求索道的长(结果精确到);(2)、求水平距离的长(结果精确到).