湖南省衡阳市衡山县2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，满分36分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. $- 2023$ 的倒数是（）

A、2023 B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 我国第一艘航母“辽宁舰”最大排水量为67500吨，用科学记数法表示这个数字是( )

A、6.75×10³吨 B、67.5×10³吨 C、6.75×10⁴吨 D、6.75×10⁵吨

查看试题解析
3. 在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这说明了（）

A、点动成线 B、线动成面 C、面动成体 D、两点确定一条直线

查看试题解析
4. 在数 $0.73$ ， 0， $- 39$ ， 1， $1 \frac{1}{2}$ ， $- \frac{3}{61}$ ， $2.43$ ， $- \frac{6}{5}$ ， $23 %$ ， 98， $\frac{π}{3}$ 中，分数有（）个．

A、4 B、5 C、6 D、7

查看试题解析
5. 下列各式中，符合代数式书写要求的是（）．

A、 $x \times 5$ B、 $4 m \times n$ C、 $1 \frac{2}{3} x$ D、 $- \frac{1}{2} a b$

查看试题解析
6. 若一个算式中， $- 3$ 是底数，4是指数，则这个算式是（　　）

A、 $- 3^{4}$ B、 ${(- 3)}^{4}$ C、 $- 4^{3}$ D、 ${(- 4)}^{3}$

查看试题解析
7. 已知 $x - 2 y = - 1$ ，则 $- 4 x + 8 y + 15$ 的值是（　　）

A、11 B、14 C、10 D、19

查看试题解析
8. 某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小．能正确解释这一现象的数学知识是（）

A、经过一点有无数条直线 B、两点确定一条直线 C、两点之间线段最短 D、垂线段最短

查看试题解析
9. 如图， $4$ 个三角形均为等边三角形，将图形沿中间三角形的三边折叠，得到的立体图形是（　　）

A、三棱锥 B、圆锥 C、四棱锥 D、三棱柱

查看试题解析
10. 如图，直线 $a ∥ b$ ， $R t △ A B C$ 的直角顶点A落在直线a上，点B落在直线b上，若 $∠ 1 = 15 °$ ， $∠ 2 = 25 °$ ，则 $∠ A B C$ 的大小为（）

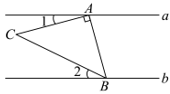A、50° B、45° C、40° D、35°

查看试题解析
11.
下列所示的四个图形中，∠1和∠2是同位角的是（）

A、②③ B、①②③ C、①②④ D、①④

查看试题解析
12. 下列图是由一些相同的小正方体搭成的几何体的三视图，则组成该几何体的小正方体的个数为（）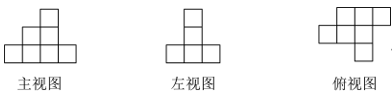

A、7 B、8 C、9 D、10

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

13. 单项式 $- 2^{4} a^{3} b$ 的次数是．

查看试题解析
14. 用“ $>$ ”、“ $<$ ”或“ $=$ ”填空： $3.15 °$ $3 ° 1 5^{'}$ ．

查看试题解析
15. 若 $2 x^{2} y^{n} - 5 x^{m} y^{3}$ 是单项式，则 $(m - n)^{n}$ ＝．

查看试题解析
16. 甲看乙的方向为北偏东 $3 0^{∘}$ ，那么乙看甲的方向是．

查看试题解析
17. 若a ， b互为相反数，c ， d互为倒数，x的平方是1，则 $a - \frac{1}{c d} + b - x^{2022}$ 的值为．

查看试题解析
18. 如图，下列条件中：
① $∠ B + ∠ B C D = 180 °$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ B = ∠ 5$ ，
能判定 $A B ∥ C D$ 的条件有（填序号）．

查看试题解析

三、解答题（本大题共6小题，第19题18分，20题8分，21题8分，22题10分，23题10分，24题12分，满分66分．解答写出文字说明、推理过程或演算步骤）

19. 计算

(1)、 $(- 5) + (- 6) - (+ 12) - (- 7)$

(2)、 $(- \frac{1}{4} + \frac{5}{6} - \frac{2}{9}) \times (- 36)$

(3)、 $- 2^{2} - 3^{3} \times (- 1)^{2022} - (- 1)^{2023}$

查看试题解析
20. 先化简，再求值． $(4 x^{2} - 2 x y + y^{2}) - 3 (x^{2} - x y + 5 y^{2})$ ，其中 $x = - 1$ ， $y = - \frac{1}{2}$ ．

查看试题解析
21. 如图，点 $O$ 是直线 $C E$ 上一点，以 $O$ 为顶点作 $∠ A O B = 90 °$ ，且 $O A$ 、 $O B$ 位于直线 $C E$ 两侧， $O B$ 平分 $∠ C O D$ ．

(1)、当 $∠ A O C = 70 °$ 时，求 $∠ D O E$ 的度数．

(2)、请你猜想 $∠ A O C$ 和 $∠ D O E$ 的数量关系，并说明理由．

查看试题解析
22. 数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们进行推理，获得结论．初中数学里的一些代数恒等式，很多都可以借助几何图形进行直观推导和解释．请结合相关知识，解答下列问题：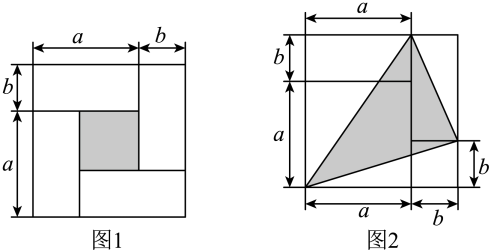

(1)、如图1是由4个大小相同，长为a、宽为b的长方形围成的边长为 $(a + b)$ 的正方形，用含字母a，b的代数式表示出阴影部分的面积．
①通过计算阴影部分正方形的边长，求阴影部分的面积，可列代数式：；
②通过用较大正方形的面积减去4个小长方形的面积，求阴影部分的面积，可列代数式：；

(2)、根据图1中的阴影部分的面积关系写出一个代数恒等式：；

(3)、若 $a + b = 6$ ， $a b = 8$ ，求图2中阴影部分的面积．

查看试题解析
23. 如图，观察下列几何体并回答问题．

(1)、请观察所给几何体的面、棱、顶点的数量并归纳出 $n$ 棱柱有个面，条棱，个顶点； $n$ 棱锥有个面，条棱，个顶点；

(2)、所有像三棱柱、四棱柱、六棱柱、三棱锥等这样由四个或四个以上多边形所围成的立体图形叫做多面体，经过前人们归纳总结发现，多面体的面数 $F$ ，顶点个数 $V$ 以及棱的条数 $E$ 存在着一定的关系，请根据（1）总结出这个关系为．

查看试题解析
24. A ， B两个动点在数轴上同时做匀速运动，运动方向不变，它们的运动时间和在数轴上的位置所对应的数记录如表．

(1)、根据题意，填写下列表格：
时间（秒）
0
5
7
A点在数轴上的位置
10
0
▲
B点在数轴上的位置
▲
12
20

(2)、A、B两点在秒时相遇，此时A、B点对应的数是；

(3)、在A、B两点上分别安装一个感应器，感应距离为3至8（即当两点距离大于等于3，小于等于8时会一直发出震动提示，距离太远或太近都不提示）．
①A、B两点开始运动后，经过几秒感应器开始发出提示？第一次提示持续多长时间？
②A、B两点开始运动后，经过几秒感应器开始发出第二次提示？

查看试题解析

时间（秒）	0	5	7
A点在数轴上的位置	10	0	▲
B点在数轴上的位置	▲	12	20